Inscription / Connexion Nouveau Sujet
L'inversion
Bonjour à tous,
Je suis face à un exercice qui me pose beaucoup de difficulté dans la mesure où je découvre l'inversion… Quelqu'un pourrais t-il m'éclairer ?
P : plan affine
O un point de P
P*=P\{O}
P est muni d'un repère orthonormé direct d'origine O.
K est un réel strictement positif
On appelle inversion de centre O et de rapport k l'application i de P* vers lui-même qui au point M associe le point M' tel que : OM'(vecteur) = k OM (vecteur) / OM²
1. J'ai réussi à faire la première question qui me demandais de déterminer les points invariants de i.
OM=kOM/OM²
OM scalaire OM=(k OM/OM²)scalaire OM
OM²=k OM²/OM²
OM²=k
donc c'est un cercle de centre O et de rayon racine de k.
2. Ensuite, on me demande de montrer que i est une involution de P* :
J'arrive à démarrer mais pas vraiment à répondre à la question…
i[OM']=k OM'/OM²
et je veux arriver à : OM''=OM
3. Là les choses commencent à se gâter …
M , de coordonnées cartésiennes (x ;y) et de coordonnées polaire (théta ; rho), est un point de P*.
On me demande de donner les coordonnées cartésiennes et polaires de M'=i(M) en fonction de celle de M.
4. Je sais que l'image, noté i (T) par l'application i d'un sous ensemble gama du plan est l'ensemble des images par i des points de Gama .
I (T)= {i(M) tel que M appartiennent à gama}.
a. D est un droite passant par O privée de O.
Je dois montrer que l'image de D par l'inversion i est elle-même.
b. D ne passe pas par O.
Je dois montrer que l'image de D par l'inversion de i est incluse dans un cercle passant par O privé de O.
Ensuite, il faut préciser la position de la droite passant par O et le centre de ce cercle relativement à D.
Enfin, il faut montrer que l'image de D est égale à ce cercle privé de O.
c. Montrons que l'image d'un cercle C passant par O privé de O est un droite ne passant pas par O et précisons la direction de cette droite.
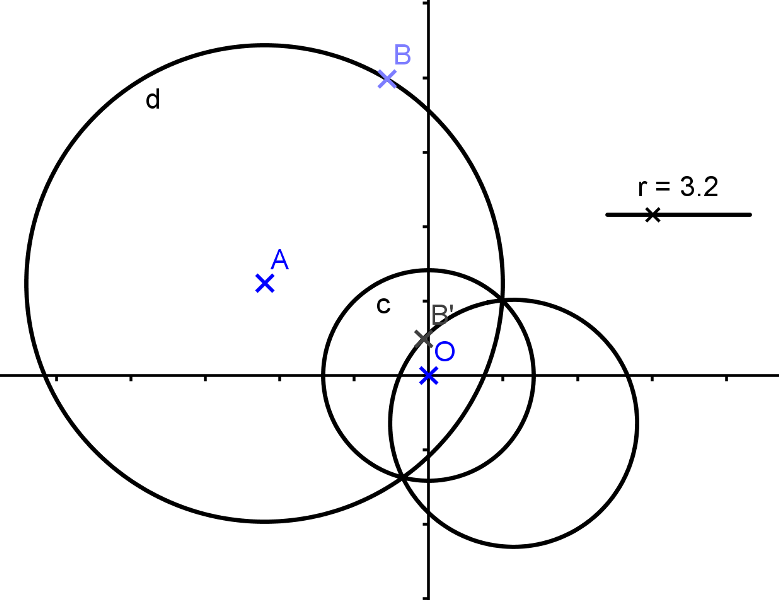
d. Montrons que l'image d'uncercle de centre oméga ne passant pas par O est un cercle de centre oméga' ne passant pas par O. Que peut on dire de O, Oméga et oméga' ?
5. Si M' et N' sont les images de M et N par l'inversion i, montrons que :
M'N'= k MN/ (OM*ON).
Merci d'avance à ceux qui prendront un peu de leur temps pour me donner un coup de main…
salut
1) ce n'est pas "un cercle" c'est "LE cercle"
2) ne veut rien dire
posons B=i(A) et C=i(B)
OB=kOA/OA² 
OB.OA=(kOA²)OA.OA=k donc OB.OA=k
de même OC.OB=k
or O,A et B sont alignés d'une part et O,B et C sont alignés donc O, A, B et C sont alignés et A=C
3) le fait que O, A et B sont alignés te permet de travailler d'abord en coordonnées polaires puis ensuite transforme en coordonnées cartésiennes
4a) trivial d'après 3)
b) cherche un peu
c)d) utilise le fait que i est involutive
5) produit scalaire et relation de Chasles
...
Salut j'ai un exo quasi identique a faire.
jai fait la 1 la 2 mais pour la 3 j'ai un doute pour les coordonnées.
3. je trouve
pour les polaires
x'=(k/
)cos
y'=(k/)sin
ou ca
'=(k)/²
'=k/
pour les cartesiennes
x'=kx/(x²+y²)
y'=ky/(x²+y²)
sinon pour la 4a
si les coordonnées sont bonnes
on aurait l'equation de la droite D : =d
ainsi '=(kd)/²
ce serait l'image de D par l'inversion i car d'autre part '=(k)/²
non?
Bonjour !
Pour les coordonnées je suis vraiment pas sûr.
En fait je trouve aussi
Cartesiennes
x'=kx/(x²+y²)
y'=ky/(x²+y²)
Polaires
x'=(k/)cos
y'=(k/)sin
ou ca
'=(k)/²
'=k/
ou encore
'cos'=cos/
'sin'=sin/
en fait je suis pas sur des coordonnées de vectOM
(,)
ou (cos,sin)
Pour la 4b j'ai fait un dessin
j'ai mis H projeté orthogonal de O sur D
ainsi OH.HM=0
ca me donne une équation cartésienne de D
je remplace dans cette equation x et y par leurs expressions en fonction de x' et y' je trouve pas d'equation de cercle
jai aussi essayé en polaires, marche pas non plus
pour la c
on a vu en b que l'image d'une droite ne passant pas par O est un cercle privé de O
comme i est involutive l'image de ce cercle est une droite ne passant pas par O
direction?
pour la d
premiere partie ?
O 
et ' alignés?
pour l'image d'un cercle ne passant pas par O utilise les coordonnées cartésiennes en écrivant
x=a+rcost
y=b+rsint
où (a,b) sont les coordonnées du centre et r le rayon puis calcule x' et y'
si (r,t) sont les coordonnées polaires de M alors (k/r,t) sont les coordonnées de M'
voici comment j'ai rédigé cela
4a
D:=d
or M'(,k/) d'où M'(d,k/) vectOM et vectOM' colinéaires et de m^m sens
or OM vect directeur de D donc OM' vect dir de l'image de D : i(D)=D
b
D:sin(-d)=norme de OH avec H prgt orth de O sur D
OH.HM=0 cercle passant par O de centre H
donc D incluse dans ce cercle par i
Annuler
connectez vous
géométrie en post-bac