Inscription / Connexion Nouveau Sujet
L octogone!!
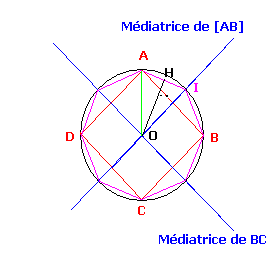
Soit un carré ABCD inscrit dans un cercle C de centre O et de rayon r.La médiatrice du segment AB coupe le cercle C en I.On note H le milieu de AI
a) Construire l'octogone regulier,inscrit dans le cercle
b)Calculer le coté IA de l'octogone,puis OH en fonction du R
c)Determiner la mesure en radians de l'angle geometrique AOH
d)En deduire cos pi/8 et sin pi/8
apres construction de la figure je ne sais pas comment faire pour deboucher sur les autres questions de l'exercice merci d'avance si vs avez une piste pour moi!
IA² = AO² + OI² - 2.AO.OI.cos(AOI)
IA² = R² + R² - 2R².cos(Pi/4)
IA² = R² + R² - V2.R² (Avec V pour racine carrée).
IA² = R².(2-V2)
IA = R.V(2-V2)
OH² + HI² = OI²
OH² + (IA/2)² = OI²
OH² + R²(2-V2)/4 = R²
OH² = R²(1 - (2-V2)/4)
OH² = R²(4 - (2-V2))/4
OH² = R²(2+V2)/4
OH = (1/2).R.V(2+V2)
-----
Angle(AOH) = 2.Pi/16 = Pi/8
-----
OH = AO.cos(AOH)
(1/2).R.V(2-V2) = R.cos(AOH)
cos(Pi/8) = (1/2).V(2+V2)
---
sin²(Pi/8) = 1 - cos²(Pi/8)
sin²(Pi/8) = 1 - (2+V2)/4
sin²(Pi/8) = (4 - (2+V2))/4
sin²(Pi/8) = (2-V2)/4
sin(Pi/8) = (1/2).V(2-V2)
-----
Sauf distraction. 
Annuler
connectez vous