Bonsoir à tous,
j'ai besoin d'aide pour finir un exercice.L'énoncé est le suivant :
Pour tout entier n 1, on pose u_n = S_n - ln(n), c'est dire un = 1 + 1/2 + 1/3 + ... + 1/n - ln(n)

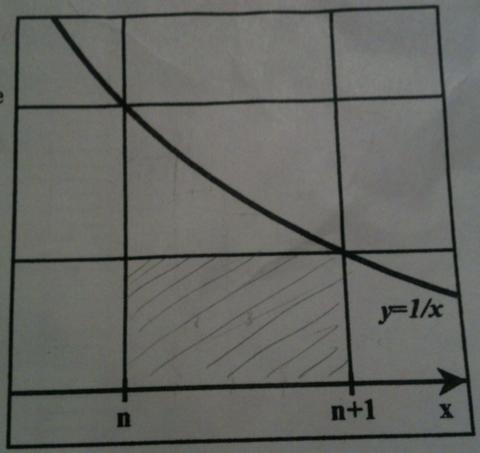
-Trouver un encadrement de l'intégrale de n à n+1 de 1/x dx
-Calculer l'intégrale

On admet le théorème "toute suite décroissante minorée admet une limite"

-Pouvez vous appliquer ce théorème à la suite u_n ?

On sait que u_n correspond à la différence entre Sn ( la série harmonique ) et ln(n) ( le logarithme népérien ). Donc un encadrement de l'intégrale serait-il un encadrement par les intégrales de ces deux fonctions ?

Merci de votre aide