Inscription / Connexion Nouveau Sujet
La droite dans le plan seconde
Bonsoir tout le monde, s'il vous plaît j'ai besoin d'aide concernant des exercices de maths ci dessous:
Ex1:
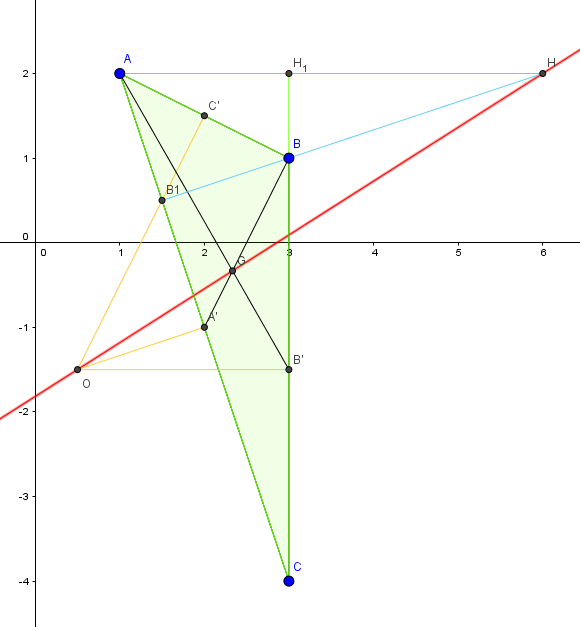
Le plan est muni d'un repère orthonormé. On considère les points suivants: A(1;2), B(3;1), C(3;4) et D(9;1).
1) Montrer que les pts A, B et C ne sont pas alignés ( j'ai déjà répondu à cette question)
2 ) Déterminer une équation cartésienne de chacune des médiatrices des côtés du triangle ABC; en déduire les coordonnées du centre O du cercle (C) circonscrit au triangle ABC et le rayon de ce cercle.
3) a/ Déterminer une représentation paramétrique de la hauteur issue de A du triangle ABC
b/ Donner une équation cartésienne de la hauteur issue de B du triangle ABC
c/ En déduire les coordonnées de l'orthocentre H du triangle ABC.
4) a/ Déterminer une représentation paramétrique de la médiane relative au sommet A du triangle ABC
b/ Donner une représentation paramétrique de la médiane relative au sommet C du triangle ABC
c/ En déduire les coordonnées du centre de gravité G du triangle ABC.
5) a/ Montrer que les points O, G et H sont alignés
b/ Déterminer la position du pt G sur le segment [OH]
c/ Montrer que( les vecteurs) OH=OA+OB+OC
6) Montrer que le triangle BCD est un triangle rectangle
7) Montrer que le quadrilatère ABCD est un trapèze
8) Donner les équations cartésiennes des droites (AC), (BD), (AD) et (BC)
9) Soient I et J les milieux respectifs de [CD] et de [AB]; soit K le point d'intersection de (BC) et (AD), soit L celui de (AC) et (BD)
a/ Détérminer les coordonnées des pts I, J, K et L
b/ Montrer que les pts I, J, K, et L sont alignés
Voilà, si quelqu'un peut m'aider il me sauvera certainement la vie :/
Question 2
La médiatrice de [BC] est facile à trouver
ensuite tu peux chercher ,par exemple celle de [AB] en écrivant MA=MB
ensuite tu cherche le point d'intersection
Donne tes réponses avant d'aborder le reste
la médiatrice de [AB] est l'ensemble des points équidistants de A et B
donc l'ensemble des points M(x,y) tels que MA=MB
(écris plutôt MA²=MB² développe et réduis)
autre méthode:
c'est la droite passant par le milieu de [AB] (à déterminer) et orthogonale à AB
(cherche le vecteur AB puis un vecteur orthogonal
le résultat que j'ai obtenu est 4x-5=0 mais est ce une équation cartésienne? parce que sa forme est ax+by+c=0 , c'est plutôt une équation réduite sous la forme mx+p=0
Bonjour tout le monde, s'il vous plaît j'ai besoin d'aide concernant cet exercice de maths , s'il vous plaît si vous pouvez m'aider , je dois le rendre ce lundi 
EXERCICE :
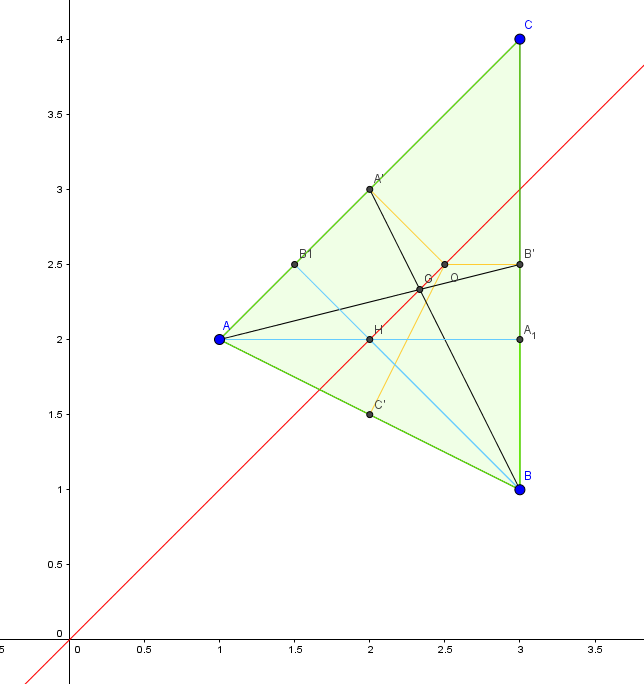
Le plan est muni d'un repère orthonormé. On considère les points suivants: A(1;2), B(3;1), C(3;4) et D(9;1).
1) Montrer que les pts A, B et C ne sont pas alignés ( j'ai déjà répondu à cette question)
2 ) Déterminer une équation cartésienne de chacune des médiatrices des côtés du triangle ABC; en déduire les coordonnées du centre O du cercle (C) circonscrit au triangle ABC et le rayon de ce cercle.
3) a/ Déterminer une représentation paramétrique de la hauteur issue de A du triangle ABC
b/ Donner une équation cartésienne de la hauteur issue de B du triangle ABC
c/ En déduire les coordonnées de l'orthocentre H du triangle ABC.
4) a/ Déterminer une représentation paramétrique de la médiane relative au sommet A du triangle ABC
b/ Donner une représentation paramétrique de la médiane relative au sommet C du triangle ABC
c/ En déduire les coordonnées du centre de gravité G du triangle ABC.
5) a/ Montrer que les points O, G et H sont alignés
b/ Déterminer la position du pt G sur le segment [OH]
c/ Montrer que( les vecteurs) OH=OA+OB+OC
6) Montrer que le triangle BCD est un triangle rectangle
7) Montrer que le quadrilatère ABCD est un trapèze
8) Donner les équations cartésiennes des droites (AC), (BD), (AD) et (BC)
9) Soient I et J les milieux respectifs de [CD] et de [AB]; soit K le point d'intersection de (BC) et (AD), soit L celui de (AC) et (BD)
a/ Détérminer les coordonnées des pts I, J, K et L
b/ Montrer que les pts I, J, K, et L sont alignés
*** message déplacé ***
Bonjour
question 2 soit produit scalaire soit
la médiatrice du segment [AB] est l'ensemble des points M tels que MA=MB
donc écrivez
*** message déplacé ***
ben voyons....on peut tout refaire aussi.....
 il (elle ) a eu des réponses, et reposte.....
il (elle ) a eu des réponses, et reposte.....
tu as lu ceci ? 
Je suis en seconde et on a pas étudié le produit scalaire y a t il un autre moyen pour répondre à cette question ?
alors pourquoi la 2e fois tu as posté en 1re ?....si tu avais lu le règlement, tu saurais qu'on ne peut pas supprimer....j'ai eu des réponses, je supprime et je recommence...tu te fiches du monde là ?
sans produit scalaire : utiliser la notion de distance, les équations de droite....
Premièrement, vous ne m'avez pas répondu concernant l'exercice. Deuxième chose, oui je n'ai pas lu le règlement j'avoue, mais ça ne se reproduira jamais. Troisième chose calme toi, au lieu de t'énerver aide moi plutôt à résoudre cet exercice si tu en a la moindre idée n'hésite pas!! Merci
Merci à vous Manny06 et Hekla, après avoir refait le calcul j'ai enfin trouvé l'équation en question : -4x+6y+5=0
Premièrement, vous ne m'avez pas répondu concernant l'exercice
si, faut lire ...et d'autres avaient déjà répondu avant aussi...
oui je n'ai pas lu le règlement
c'est un tort....
Troisième chose calme toi, au lieu de t'énerver aide moi plutôt
je t'ai aidé mais tu n'as pas lu...et personnellement je suis plus que réservée pour aider les personnes qui ne respectent pas le règlement....
quant au rôle d'un modérateur sur un site, ce n'est pas toi qui va me l'apprendre
malou (=modérateur)
Moi aussi ,je suis d'accord
tu peux faire la même chose pour les autres médiatrices même si je t'ai indiqué que pour celle de [BC] c'était plus facile (BC est verticale donc la médiatrice est l'horizontale passant par le milieu de [BC] équation ?)
médiatrice de [BC]
en dehors du fait que cela se simplifie le milieu de [BC] a pour ordonnée
comme (BC) est parallèle à l'axe des ordonnées la perpendiculaire à (BC) est parallèle à l'axe des abscisses
la médiatrice cde [BC] a pour équation ou
pour celle de [AC]
Pour trouver les coordonnées du pt O centre du cercle circonscrit au triangle ABC (le pt d'intersection des des trois médiatrices) je dois mettre l'égalité de deux équations par exemple (d1):4x-2y-5=0<=>y=2x-5/2 et (d2):4x+4y-20=0 <=>y=5-x
d'où: 2x-5/2=5-x
x=5/2 et puis je remplace par la valeur de x dans l'une des deux équations pour trouver y; y=5/2 donc les coordonnées de O sont (5/2;5/2) ?
vous n'avez pas lu mon précédent message revoyez vos calculs
oui il suffit de choisir deux médiatrices une s'impose
résolvez
je n'ai pas compris comment vous avez fait pour trouver l'ordonnée
car les coordonnées d'un milieu on les trouvent par la formule( x1+x2/2; y1+y2/2 )
si j'applique ceci ,le milieu de [BC] a pour ordonnée 1+4/2=5/2
donc y=5/2 <=> 2y-5=0