Inscription / Connexion Nouveau Sujet
La représentation graphique des fonctions
Bonjour
J'aurais besoin d'aide pour cet exercice.
L'énoncé:
Le plan est muni d'un repère orthogonal ,( Cf) est la courbe représentative d'une fonction f, d'ensemble de définition [-3/2 ; 9/2]
1. Construire la courbe représentative (Cg) de la fonction g:
g: x → f(x+3/2) -2.
2. Construire la courbe représentative (Ch) de la fonction
h: x → f(-x).
3. Déduire de ( Cf) et de ( Cg) la représentation graphique de la fonction x → f(|x|).
Merci de m'expliquer je ne comprends pas bien 
Bonjour beug
Je vois que tu travailles beaucoup.
1. Construire la courbe représentative (Cg) de la fonction g:
l'as-tu construite?
Bonjour Beugg.
Je suppose qu'il doit s'agir d'une construction théorique ? Vu que je n'ai pour seul renseignement sur f que son domaine de définition (La fonction f peut être absolument irreprésentable, genre indicatrice de  )
)
La première question que tu doir te poser pour 1. et 2. est la suivante :
"quel sont les domaine et image de mes fonction g et h ?" (Ok ça fait deux questions en une, désolé  )
)
Donc, répondez déjà à ça.
Cordialement,
Bonjour
je pense que beugg peut aussi s'aider d'un croquis pour comprendre ce qui se passe...
je fais un petit croquis d'une courbe Cf (courbe de f) entre -3/2 et 9/2 (obligatoire)
1. Construire la courbe représentative (Cg) de la fonction g:
g: x → f(x+3/2) -2
g:x
 ....
....
-->donc je choisis un x sur l'axe des abscisses
-->je vais chercher alors x+3/2 sur l'axe des abscisses
-->qui a une image par f (grâce à la courbe Cf)
--> à cette image, j'enlève 2. J'obtiens une ordonnée.
cette valeur trouvée me donne le point image de x par g
Bon, je voulais juste emmener Beugg sur les points que vous abordez, mais en le laissant réfléchir ...
Merci pour votre réponse
En réalité j'ai la représentation de f dans l'énoncé,sauf je n'arrive vraiment pas à retracer Cf avec logiciel comme "sine qua non"
Ce qui compte surtout, c'est la démarche que t'a donné Malou.
Je déplace à droite, à gauche, pourquoi ?
Je le monte, je descends, pourquoi ?
Dois-je faire faire des réductions, des agrandissements, pourquoi ? ( ex : tracer f(2x) ou f(x/2))
etc etc
Après, ma foi, déplacer un graphique selon cette démarche n'a plus rien de sorcier.
voici un exemple en image, si je ne me suis pas trompée ! ça peut arriver !
applique sur ce dessin, mes explications de 15h16 (mais ne saute aucune ligne !! )
je suis partie du point P de l'axe des abscisses
....
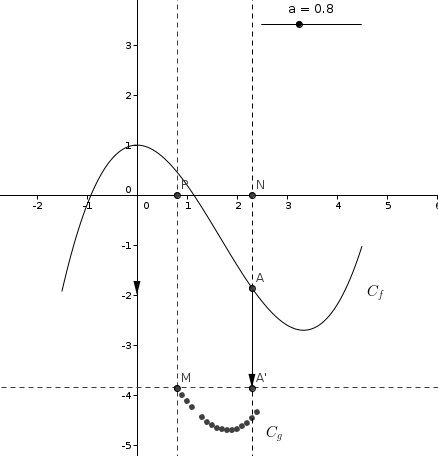
c'est ce qu'on appelle construire une courbe point par point
Bonjour
Malou j'ai compris votre démarche.Mais comme on n'a pas ,à peu près,la même courbe (dans l'énoncé) ,il est difficile de continuer cette construction de Cg
Mais la démarche reste toujours valable...
Par exemple, avec votre courbe
Quand x= 0,9 , on aurait x +3/2= 2,4
Donc f(x+3/2)= -2
Alors g(x)= f(x+3/2) -2= =-4 , ainsi de suite jusqu'avoir la Cg ?
salut
beugg a déjà fait le même genre d'exercice ici ![]() Tableau de variations avec un tableau de variation ....
Tableau de variations avec un tableau de variation ....
celui-ci est plus simple puisqu'on a une courbe ...
mais comme pour l'exercice de l'autre fil la première chose est de répondre à la question de jsvdb de 15h08 ...
un conseil : faire des exercices et travailler c'est bien ... mais en faire trop sans assimiler les principes et savoir-faire de base n'est pas travailler ...
l'objectif de l'apprentissage c'est de repartir avec des choses dans la poche ...

Merci carpediem pour ce conseil 
Donc on va répondre à la question de jsvdb :
"Quels sont les domaines et images de mes fonctions ? "
g(x)= f(x+3/2)-2
Tel que x+3/2  Df
Df
Donc g est définie sur [-3; 3]
L'image de x par g est f(x+3/2)-2
h(x)= f(-x)
Tel que -x  Df
Df
Donc h est définie sur [-9/2; 3/2]
L'image de x par h est f(-x)
C'est bon ?
Merci d'avance 
en plus avec geogebra tu pourrais tout voir
tu prends par exemple :
f(x) = 2x^3 - 5x^2 + 1 (que tu définis sur l'intervalle [-2, 3] par exemple
puis ensuite tu construis les fonctions :
g(x) = f(-x)
h(x) = -2f(x) + 3
i(x) = f(-2x + 3)
...
et tu regardes et tu réfléchis ...
Donc g est définie sur [-3; 3]
Donc h est définie sur [-9/2; 3/2]
Impeccable.
L'image de x par g est f(x+3/2)-2
L'image de x par h est f(-x)
Ce n'est pas l'image de x qui m'intéresse ici.
C'est bien une image, mais laquelle ?
Excuses moi, je n'ai pas été clair.
Ce qu'il faut trouver maintenant, c'est le "cadre" graphique dans lequel évoluent les fonctions g et h.
Donc ce que je souhaitais te faire faire, c'était trouver les images, par g et h, de leur ensemble de départ que tu as trouvés.
g([-3, 3]) = ...
h([-9/2; 3/2]) = ...
En plus d'après ma figure,
On a pour les extréma de f respectivement:
2,5 ; -2; 0 ; 1; -1,7
Donc
f: x+3/2 de [ -3/2, 9/2] ----> f (x+3/2) de [-2; 2,5]
g([-3;3])= f([-3; 3])-2
h([-9/2; 3/2])= f([-9/2;3/2]) ?
Non !
f est définie sur [-3/2; 9/2]. Cela ne peut pas changer.
Donc :
g([-3;3])= f( [-3/2; 9/2]) - 2
h([-9/2; 3/2])= f([-3/2;9/2])
Donc on déduit :
- que g a un graphique dont dont chaque point a une abscisse comprise entre -3 et 3 et une ordonnées qui est celle de f - 2.
Un point (x, y) de (Cf) va donner naissance à un point de (Cg) de coordonnées (x - 3/2, y -2)
(Cg) est donc obtenu en translatant (Cf) par le vecteur (-3/2, -2)
- que h a un graphique dont chaque point a une abscisse comprise entre -9/2 et 3/2 et une ordonnée qui est la même que f.
Un point (x,y) de (Cf) va donner naissance à un point de (Ch) de coordonnées (-x, y)
(Ch) est donc obtenu à partir de (Cf) par réflexion par rapport à l'axe des ordonnées.
Merci jsvdb pour toutes ces explications
je comprends mieux parce qu'on n' avait pas déterminé les domaines de définition pour g et h.
Ok ce que je n'ai pas compris c'est : Cg de cordonnées (x-3/2; y-2)
D'où vient ce x-3/2 ?
Ainsi ,construire une courbe par la translation du vecteur (-3/2 ;-2), merci de m'expliquer la technique
Eh bien, pour un x donné dans le domaine de g, c'est-à-dire [-3, 3], comment vais-je déterminer la valeur y qui lui correspond, savoir g(x) ?
La seule indication que j'ai, c'est g(x) = f(x+3/2) - 2.
Donc, je prend mon x, je lui ajoute 3/2. J'atterris dans le domaine de f (la seule que je connaisse)
Pour calculer y : je pars de x + 3/2 et je calcule f(x + 3/2). Là, je suis dans l'image de f.
Je retranche 2 à y et j'atterris dans l'image de g : J'ai trouvé mon g(x).
Alors maintenant je prends un (x, y) sur (Cf).
Question : à quel point de (Cg) va t il donner naissance ?
Réponse : je fais la démarche inverse de celle de dessus.
y est dans l'image de f, je retranche 2 et je passe dans l'image de g.
x est dans le domaine de f : x - 3/2 est dans le domaine de g.
Conclusion (x, y) sur (Cf) donne naissance à (x -3/2, y - 2) sur (Cg)
Donc je dois déplacer ma courbe (Cf) de -3/2 en abscisses et de -2 en ordonnée pour avoir celle de (Cg). C'est ce que j'appelle la translation de vecteur (-3/2, -2) de la courbe (Cf).
Oui effectivement x est dans le domaine de f : x-3/2 est sans doute dans le domaine de g .Merci
Alors pour la question 3
f3 est définie donc sur [0; 9/2]
On peut dire : (x, y) sur Cf va donner naissance à (|x| , y) sur Cf3 ?
Bonjour Beugg
Non, le domaine de f3 n'est pas celui que tu indiques.
Poses toi la question : pour que f3 ait un sens, où doit se trouver x ? Autrement dit, où a le droit de se trouver x pour que f(|x|) soit défini ?
On peut dire : (x, y) sur Cf va donner naissance à (|x| , y) sur Cf3 ?
Oh non ! là c'est plus compliqué. C'est pour cela qu'on te demande de déduire
(Par contre, dans ton énoncé initial, je ne vois pas bien ce que vient faire (Cg), je pense plutôt que c'est (Ch) : 3. Déduire de (Cf) et de (Ch) la représentation graphique de la fonction x → f(|x|).
Merci jsvdb pour votre réponse 
Donc
(x, y) sur Cf va donner naissance à (-x, y) sur Cf3 , si f3 est définie sur [-3/2, 0]
(x, y) sur Cf va donner naissance à (x, y) sur Cf3 , si f3 est définie sur [0, 9/2]
C'est correct ?
Merci d'avance 
On approche de la solution. Mais ta réponse est fausse parce que tu n'as toujours pas répondu à la question fondamentale : quel est le domaine de f3 ?
Et ensuite, et seulement ensuite, tu te poseras la question de savoir quelle est l'image de f3
Et ensuite, et seulement ensuite, tu te demanderas ce que deviens un x qui est dans de le domaine de f3
Et ensuite, et seulement ensuite, tu en déduira ce à quoi donnent naissance les points de (Cf).
Si tu grilles les étapes, c'est mort !
OK jsvdb 
1/
L'image de f3 est y
2/
x est devenu positif
Donc f3 est définie sur [0, 9/2]
Ainsi ,Cf3 est déduite par Cf dans le domaine de [0, 9/2]
C'est mort ?
Merci d'avance 
Tu n'as toujours pas répondu correctement à la question fondamentale : quel est le domaine de f3 ? (je sais, je suis pénible  )
)
Le domaine de f3 = [ ... , ... ] parce que si x est dans ce domaine, f(|x|) est défini ?
Le domaine de f3= [0, 9/2]
Donc f(|x|) est définie sur [0, +
 [ ?
[ ?Ça c'est ce qu'on appelle se contredire
 .
.
Réponse :
Le domaine de f3 ?
f est défini sur [-3/2; 9/2], donc toute valeur comprise dans cet intervalle a droit à une (belle) image.
f3 n'est définie que si |x|
 [-3/2; 9/2].
[-3/2; 9/2].
Mais c'est la valeurs absolue qui est dans [0; 9/2].
Donc f3 n'est définie que si x
 [-9/2; 9/2], intervalle qui constitue donc le domaine de f3
[-9/2; 9/2], intervalle qui constitue donc le domaine de f3
L'image de f3 ?
C'est donc l'image de f, restreinte à l'intervalle [0; 9/2]. Puisque pour trouver l'image d'un x dans le domaine de f3, j'irai dans [0,9/2] et je regarderai l'image par f.
Que devient un point (x,y) qui se trouve sur (Cf) ? On note (Ci) la courbe de f3
Il y a deux cas :
1- x est négatif et il ne se passe rien (fausse couche)
2- x est positif et il donne naissance à des jumeaux : (x, y) et (-x, y) sur (Ci)
Donc, pour répondre à la question :
On déduit (Ci) de (Cf) et (Ch) par :
On prend le sous-ensemble des points de (Cf) dont l'abscisse est positive et ça nous donne la moitié droite de (Ci)
On prend le sous-ensemble des points de (Ch) dont l'abscisse est négative et ça nous donne la moitié gauche de (Ci)
(Ci) est donc symétrique par rapport à l'axe des y.
Voilà mon ami.



