Inscription / Connexion Nouveau Sujet
la suite de syracuse suite et algorithme
On considère les suites (Un) définie de la façon suivante :
Si Un est pair alors Un+1= Un/2
Si Un est impair alors Un+1= 3Un+1
1) Calculer les 9 premiers termes de la suite (Un) si u0=5
J'ai fais : U1=3x5+1=16 U2=16/2=8 U3=8/2=4 U4=4/2=2 U5=2/2=1 U6=3x1+1=4 U7=4/2=2 U8=2/2=1
2) Soit (Un) une des suites définies précédemment.
Supposons qu'il existe un entier n0 tel que Un0=1
Que peut-on dire des termes de la suite à partir de n0 ?
Je n'ai pas trop compris, j'ai dis que n0
n on dit que (Un) admet une limite en 1 lorsque quelque soit le réel n il existe un entier n0 tel que : n0n donc 1n
On dira que la suite (Un) admet pour limite 1, on peux dire que les termes à partir de n0 convergent vers 1. 
3)Algorithme :
Début :
Entrer A
Tant que A
1
Si partie décimale de A/2=0
Alors
A prend pour valeur A/2
sinon
A prend pour valeur 3A+1
Fin Si
Afficher A
Fin tant que
4) Finit-on par obtenir 1 si le premier terme de la suite est u0=3 ? u0=7 ? u0=11 ? u0=13 ? u0= 19 ? Utiliser le programme précédent pour répondre.
J'ai utiliser le programme et j'ai fini par trouver 1 pour toutes les propositions.
5) On appelle altitude la valeur k la plus grande valeur de un obtenue en prenant u0=k
a) Déterminer l'altitude de la suite du 1
J'ai dis que l'altitude est 16 donc U1
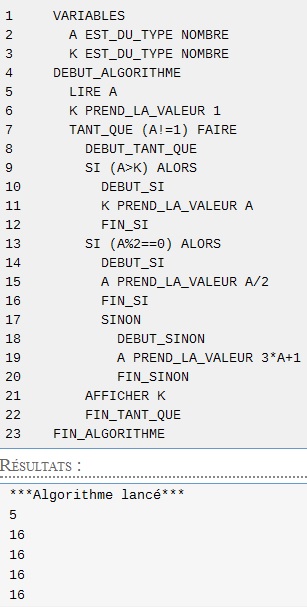
b) Modifier l'algorithme précédent pour qu'il affiche seulement l'altitude pour une valeur de u0 saisie
j'ai pas compris comment il fallait faire aider moi svp
c) Programmes l'algorithme précédent sur la calculatrice et donner les altitudes des suites du 4
Je ne l'ai pas fais vu que c'est la suite du b
6) On appelle temps de vol de la valeur k le plus petit entier n tel que un=k.
a) Déterminer le temps de vol de la suite du 1
b) Modifier l'algorithme précédent pour qu'il affiche seulement le temps de vol pour une valeur de u0 saisie
c) Programmer l'algorithme précédent sur la calculatrice et donner les temps de vols des suites du 4
La 6 je n'ai pas encore chercher
Voilà ce que j'ai trouvé pour l'instant
Serait-t-il possible de me dire si ce que j'ai déjà fait est correct, et m'aider pour la suite. S'il-vous-plaît. Merci d'avance.
Bonjour,
D'accord pour le 1)
Regarde bien sur cette liste déjà réalisée ce qui est demandé sur la question 2), et notamment ce qui concerne U5, puis ... ?
Bonjour,
1) Ok
2) tu n'as effectivement pas compris 
; ce qui t'es demandé, c'est ce qui se passe si au bout d'un certain nombre de termes tu obtiens 1. Et la réponse est que le terme suivant est 4 puis le suivant 2 et le suivant 1 et on tourne en boucle (il n'y a pas de limite qui tienne ici!) 1; 4; 2; 1; 4; 2; 1; 4; 2; 1; 4; 2; 1...
3) ??? je ne sais pas quelle est la question...
4) je te fais confiance!
5) a) oui 16 (peut importe que ce soit u1! et surtout ne pas faire précéder du donc qui peut laisser entendre je ne sais pas trop quoi)
b)
Début :
Entrer A
K prend la valeur 1
Tant que A différent de 1
K prend la valeur maximum de (A;K)
Si partie décimale de A/2=0
Alors
A prend pour valeur A/2
sinon
A prend pour valeur 3A+1
Fin Si
Afficher B
Fin tant que
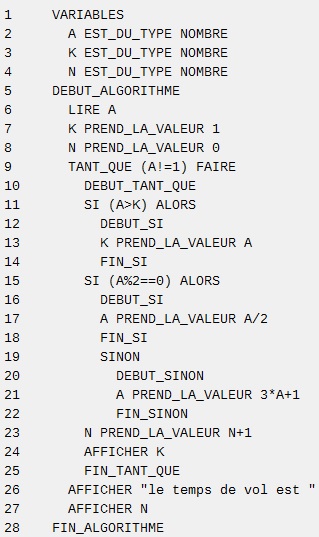
6)
Début :
Entrer A
K prend la valeur 1
N prend la valeur 0
Tant que A différent de 1
K prend la valeur maximum de (A;K)
N=N+1
Si partie décimale de A/2=0
Alors
A prend pour valeur A/2
sinon
A prend pour valeur 3A+1
Fin Si
Afficher N
Fin tant que
Il faudrait essayer les algo proposés pour vérifier (il peut y avoir un décalage de 1 par exemple pour le temps de vol (initialiser N à -1 dans ce cas!)
Merci beaucoup pour vos réponses, je n'ai pas compris d'ou vient ce B : [quote] Afficher B /quote] après le fin Si dans le 5) b)
C'est K en fait!
au début j'avais écrit avec B et c'est seulement après que j'ai vu que l'altitude était notée k; j'ai donc remplacé B par K (et j'en ai oublié un!)
max(A;K) n'est peut être pas connu. Peut etre faut-il écrire
si A>K alors K prend la valeur A à la place...
Merci beaucoup, mon problème est que je dois faire des fautes en le notant sur ma calculette, pourrais-je avoir votre site s'il vous plait afin de faire la question c) du 5) qui est de l'utiliser pour u0=3, u0=7, u0=11, u0=13 et u0=19
Merci beaucoup de votre aide
algobox n'est pas un site mais un logiciel assez basique (et simple!) qu'il faut charger sur l'ordinateur.
Attention le programme écrit donne l'altitude et pas le temps de vol!
Ah daccord je vais essayer de le télécharger alors
Oui oui, le temps de vol est pour la question 6 de toute façon
Paquet binaire "universel" pour MacOsx >=10.5 (32 bits) :
AlgoBoxMacosx32.zip - autre lien de téléchargement
Pour utiliser AlgoBox : télécharger, dézipper le fichier et lancer AlgoBox en double-cliquant sur l'icone du programme (inutile de l'installer dans le répertoire /Applications)
10.10 est >= 10.5 donc la version ci-dessus devrait fonctionner je pense...
Sinon j'ai adapté pour faire apparaître le temps de vol après les différentes étapes du seuil et ça donne
Donc récapitulatif,
5) a) l'altitude de la suite 1 est 16
b) l'algorithme que vous m'avez donner au dessus
c) altitude de u0=3 est 16
altitude de u0=7 est 52
altitude de u0=11 est 52
altitude de u0=13 est 40
altitude de u0=19 est 88
je crois que j'ai eut une erreur..
6) a) le temps de vol e la suite du 1 c'est a dire u0=5 est ..?
b) algorithme
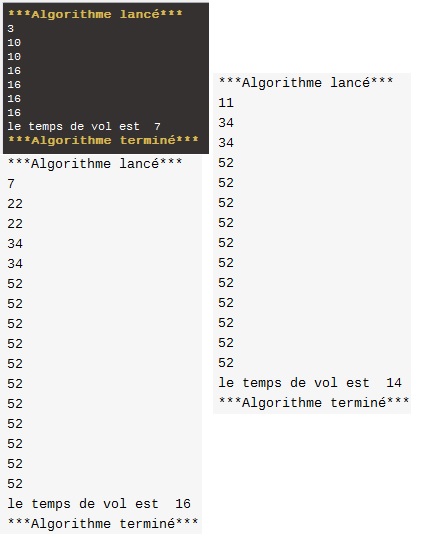
c) U0=3 le temps de vol est 7
U0=7 le temps de vol est 16
U0=11 le temps de vol est 14
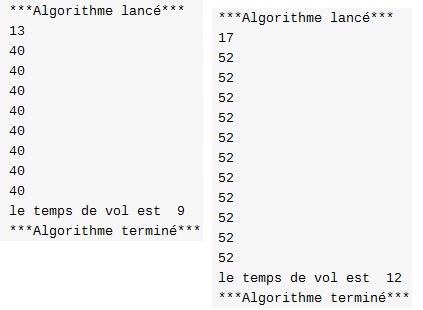
U0=13 le temps de vol est 9
U0=19 le temps de vol est 12
5) ok
6) uo = 5 donne un temps de vol de 5
c) oui sauf pour uo=19; je trouve un temps de vol de 20! (j'avais fait pour 17 au lieu de 19 dans le post précédent!) mais l'altitude est bien 88
Annuler
connectez vous