Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première VecteursTopics traitant de vecteurs [tout]Lister tous les topics de mathématiques

1 2 +

Niveau première
Partager :

le cercle d'euler

Posté par
miss_lady 26-10-08 à 15:40

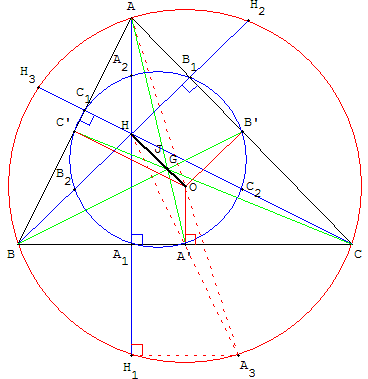
LE CERCLE D'EULER

ABC est un triangle ni isocèle ni rectangle. On appelle A' , B' et C' les milieux respectifs des côtés [BC], [CA] et [AB]. O est le centre du cercle circonscrit au triangle ABC

Soit H le point tel que : vecteur OH = vecteur OA + vecteur OB + vecteur OC

1) Démontrer que : vecteur AH = 20 vecteur A', puis démontrer que : vecteur BH = 20 vecteur B' et vecteur CH= 20 vecteur C'

2) En déduire que H est l'orthocentre du triangle ABC

3) On appelle A0 , B0 et C0 les milieux respectifs de [AH], [BH] et [CH] : Démontrer que K , le milieu de [OH], est aussi le milieu de [A0A'], de [BOB'] et de [C0C']

4) Démontrer que : vecteur KA0 = 1/2 vecteur OA, puis que : vecteur KA0 = vecteur KB0= vecteur KC0 = 1/2 vecteur OA

5) On appelle A1, B1 et C1 les pieds des hauteurs du tirangle ABC. Démontrer que le cercle de centre K et de rayon 1/2 OA passe par les 9 points nommés dans ce problème . Ce cercle s'appelle  cercle d'EULER du triangle ABC.

NB: il peut y avoir des fautes a propos des vecteurs car les flèches ne sont pas bien passés a la photocopie ; donc voila j'ai un dm a rendre où j'ai passé beaucoup de temps dessus mais je n'y arrive pas merci de m'aidé SVP J AI BESOIN DE VOTRE AIDE ....

le cercle d\'euler

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:08

Bonjour,

Où en es-tu exactement ? Dans quelles directions as-tu cherché ?

Nicolas

Posté par
pythamedere : le cercle d'euler 26-10-08 à 20:09

Citation :
1) Démontrer que : vecteur AH = 20 vecteur A', puis démontrer que : vecteur BH = 20 vecteur B' et vecteur CH= 20 vecteur C'


Je ne comprends pas cette phrase ! Toi si ?

Je suppose que tu voulais dire "Démontrer que \vec{AH} orthogonal à \vec{BC}" étant donné la question suivante : "2) En déduire que H est l'orthocentre du triangle ABC ", mais ce que tu as écrit est tellement loin de ce que je pense que tu as voulu écrire, que j'ai quelques doutes...

Posté par
miss_ladyle cerle d'euler 26-10-08 à 20:11

a vrai dire je n'y arrive pas du tou a commencé l'exercice

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:11

Il s'agit bien sûr de \vec{AH}=2\vec{OA'}

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:12

Le SMS est interdit sur ce forum !

a vrai dire je n'y arrive pas du tou a commencé l'exercice
=> à vrai dire je n'arrive pas du tout à commencer l'exercice

Je regarde...

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:13

il s'agit de  20 pas de 2

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:13

1.a.
En vecteurs :
OH = OA + OB + OC
OH - OA = OB + OC
AH = OB + OC
Or A' est le milieu de [BC]. Donc... (continue)

Posté par
miss_ladyle cercle 26-10-08 à 20:15

c'est la relation de Chasle non ?? a vrai dire je n'arrive pas avec les vecteurs c'est pour ca que j'ai passé énormement de temps sur ce dm hélas je comprend rien

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:15

Tu as lu mon message précédent ?!

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:17

oui vous avez raison il s'agit de 2 vecteur OA' et non 20

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:20

pythamede je ne comprend pas ce que tu veux dire ??

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:21

tu peux continuer a m'aidé Nicolas_75 car je ne comprends rien

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:21

1.a.
En vecteurs :
OH = OA + OB + OC
OH - OA = OB + OC
AH = OB + OC
On fait intervenir le milieu A' de [BC] :*
AH = OA' + A'B + OA' + A'C
AH = 2OA' + (A'B + A'C)
Or A' est le milieu de [BC], donc A'B + A'C = 0. Donc :
AH = 2OA'

Fais de même avec 1.b. pour voir si tu as compris.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:24

mais il n'y pas de 1.b tu veux dire la question 2 ??

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:25

Non. Je veux dire la 2ème partie de la question 1

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:28

donc la 2ème partie :

BH = 2 OB

mais les deux vecteurs sont parallèles il faut montrer une colinéarité non ??

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:29

(En vecteurs) BH n'est pas égal à 2OB mais à 2OB' !
Pour le montrer, utilise la même méthode que moi ci-dessus.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:31

a vrai dire je n'y arrive pas du tout avec les vecteurs pourrais-je avoir un peu plus de détaille

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:35

Nicolas_75 tu es bon en maths je peux avoir un peu plus d'aide de ta part ?

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:41

1.a.
\vec{OH} = \vec{OA} + \vec{OB} + \vec{OC}
\vec{OH} - \vec{OA} = \vec{OB} + \vec{OC}
\vec{AO} + \vec{OH} = \vec{OB} + \vec{OC}
\vec{AH} = \vec{OB} + \vec{OC}
On fait intervenir le milieu A' de [BC] :
\vec{AH} = \vec{OA'} + \vec{A'B} + \vec{OA'} + \vec{A'C}
\vec{AH} = 2\vec{OA'} + \left(\vec{A'B} + \vec{A'C}\right)
Or A' est le milieu de [BC], donc \vec{A'B}+\vec{A'C}=\vec{0}. Donc :
\fbox{\vec{AH} = 2\vec{OA'}}

Fais de même pour 1.b.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:51

j'arrive pas a le faire j ai pas etudié encore ce chapitre

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:51

Si tu parles du chapitre sur les vecteurs, en effet, il conviendrait que tu l'étudies avant de faire les exercices.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 20:55

ce chapitre nous devons l'étudier a la fin de l'année de seconde mais elle était absente et cette année nous avons fait un devoir où tout le monde a eu une note catastrophique et ce dm c'est un ratrapage de ce devoir or moi je n'ai pas étudié ce chapitre a cause de mon professeur qui était absente l'année dernière et cette année je comprends plus rien en maths c'est pour ça que j'avais demandé de l'aide pour ce dm et pour me rattrapé en maths

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 20:56

Apparemment, tu ne comprends pas les réponses qu'on te donne. Il est donc inutile d'aller plus loin. Les autres questions sont plus compliquées que la première, assez facile quand on connaît son cours.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 21:07

vous pouvez m'aidez sinon je vais pas pourvoir rendre mon dm de maths SVP j'ai besoin de votre aide je commence a découragé

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 21:09

Je veux bien t'aider, mais pas de faire ton DM de A à Z sans que tu comprennes.
A 20h41, je t'ai donné un raisonnement détaillé pour 1.a.
Propose un raisonnement similaire pour 1.b.
Puis nous passerons à 2.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 21:11

oui justement je vous demande une explication pour que je puisse vous donnez un raisonnement pour 1.b

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 21:13

1.a.
\vec{OH} = \vec{OA} + \vec{OB} + \vec{OC}
\vec{OH} - \vec{OA} = \vec{OB} + \vec{OC}
\vec{AO} + \vec{OH} = \vec{OB} + \vec{OC}
On applique la relation de Chasles dans le membre de gauche :
\vec{AH} = \vec{OB} + \vec{OC}
On fait intervenir le milieu A' de [BC], grâce à la relation de Chasles :
\vec{AH} = \vec{OA'} + \vec{A'B} + \vec{OA'} + \vec{A'C}
\vec{AH} = 2\vec{OA'} + \left(\vec{A'B} + \vec{A'C}\right)
Or A' est le milieu de [BC], donc \vec{A'B}+\vec{A'C}=\vec{0}. Donc :
\fbox{\vec{AH} = 2\vec{OA'}}

Fais de même pour 1.b.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 21:33

OH=OA+OB+OC
OH-OA=OB=OC
AO=OH=OB=OC
BH=OA=OC
BH=BA'+A'B+OB'+B'C
BH+2OB'+(A'B+B'C
or B'est le milieu de [CA] donc A'B+B'C= 0

est ce que c'est juste ?

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 21:42

Je n'arrive pas à lire. Trop de fautes de frappe.
Poste un texte clair

Citation :
OH-OA=OB=OC
AO=OH=OB=OC
BH=OA=OC
BH+2OB'+(A'B+B'C

Posté par
miss_ladyle cercle d'euler 26-10-08 à 21:44

OH=OA+OB+OC
OH-OA=OB=OC
AO=OH+OB=OC
BH=OA+OC
BH=BA'+A'B+OB'+B'C
BH+2OB'+(A'B+B'C)
or B'est le milieu de [CA] donc A'B+B'C= 0
BH=2OB

est ce que c'est juste ?

Posté par
miss_ladyre : le cercle d'euler 26-10-08 à 21:45

OH=OA+OB+OC
OH-OA=OB=OC
BH=OA+OC
BH=BA'+A'B+OB'+B'C
BH+2OB'+(A'B+B'C)
or B'est le milieu de [CA] donc A'B+B'C= 0

est ce que c'est juste ?

Posté par
miss_ladyle cercle d'euler 26-10-08 à 21:47

je suis désolé j'ai fait encore d'autre faute de frappe


OH=OA+OB+OC
OH-OA=OB+OC
BH=OA+OC
BH=BA'+A'B+OB'+B'C
BH+2OB'+(A'B+B'C)
or B'est le milieu de [CA] donc A'B+B'C= 0

est ce que c'est juste ?

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 21:49

Non.

1.b.
\vec{OH} = \vec{OA} + \vec{OB} + \vec{OC}
\vec{OH} - \vec{OB} = \vec{OA} + \vec{OC}
\vec{BO} + \vec{OH} = \vec{OA} + \vec{OC}
On applique la relation de Chasles dans le membre de gauche :
\vec{BH} = \vec{OA} + \vec{OC}
On fait intervenir le milieu B' de [AC], grâce à la relation de Chasles :
\vec{BH} = \vec{OB'} + \vec{B'A} + \vec{OB'} + \vec{B'C}
\vec{BH} = 2\vec{OB'} + \left(\vec{B'A} + \vec{B'C}\right)
Or B' est le milieu de [AC], donc \vec{B'A}+\vec{B'C}=\vec{0}. Donc :
\fbox{\vec{BH} = 2\vec{OB'}}

Posté par
miss_ladyle cercle d'euler 26-10-08 à 21:54

ok merci beaucoup puis-je avoir d autre piste pour la suite ?

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 21:57

Réponds aux deux questions suivantes et je t'aiderai pour 2. :
a) L'orthocentre est l'intersection des trois ...
b) O est le centre du cercle circonscrit, donc l'intersection des trois ...

Posté par
miss_ladyle cercle d'euler 26-10-08 à 22:00

a) l'orthocentre est l'intersection des trois hauteurs
b) O est le centre du cercle circonscrit, donc des trois hauteurs issus de chaque points


est ce que c'est juste ?

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 22:01

Citation :
b) O est le centre du cercle circonscrit, donc des trois hauteurs issus de chaque points

Faux. Relis ton cours de collège et réponds correctement à cette question simple.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 22:05

b) O est le centre du cercle circonscrit, donc l'intersection des trois vecteurs  

est ce que cette fois c'est juste ?

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 22:06

Non.

Posté par
miss_ladyre : le cercle d'euler 26-10-08 à 22:06

O est le centre du cercle circonscrit, donc l'intersection des trois médianes ??  

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 22:07

Non.

Posté par
miss_ladyre : le cercle d'euler 26-10-08 à 22:08

O est le centre du cercle circonscrit, donc l'intersection des trois points ??  

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 22:09

Non.
Je ne comprends pas : des vecteurs n'ont pas d'intersection ! des points non plus !

Je te pose une question simple niveau collège :
O est le centre du cercle circonscrit, donc l'intersection des trois ... du triangle.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 22:11

O est le centre du cercle circonscrit, donc l'intersection des trois bisectrices du triangle  ABC.

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 22:12

Non. Arrête de faire des réponses au hasard. Apprends ton cours. Puis reviens avec une réponse sérieuse. Je me déconnecte dans 15 minutes.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 22:15

je n'ai pas de cours justement et ça je n'ai pas reussi a te le faire comprendre
notre professeur de l'année dernière est tombé malade et n'a pas fini le programme je n'ai jamais étudié ce cours la avec les vecteurs et cette  année je suis embêté je n'arrive pas a faire mon DM c'est pour ça que j'avais demandé de l'aide et mes réponses n'etaient pas au hasard

Posté par
Nicolas_75 Correcteurre : le cercle d'euler 26-10-08 à 22:18

Je ne te parle pas de ton cours de Seconde, mais de ton cours de collège.
Mon offre tient toujours.
O est le centre du cercle circonscrit, donc l'intersection des trois ... du triangle.
Et je te donne la réponse à 2.

Posté par
miss_ladyle cercle d'euler 26-10-08 à 22:22

écoute j'ai bien réflechi je pense que c'est les trois bissectrices ça ne peut pas être autre chose car A', B' , C' sont les milieux et les droites perpendiculaires à chaque côtés passant par le milieu de chasue côtés se croisent en O

il manque une partie de la réponse 1 a faire donc la 1.c CH=2OC

1 2 +


Rechercher
Menu
Espace membre
5 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1733 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !