Inscription / Connexion Nouveau Sujet
Le chemin le plus court - Théorème de Pythagore
Bonjour, j'ai un exercice de recherche de mathématiques à rendre mais je n'y arrive pas.
Voilà l'énoncé :
Sachant que l'on ne peut emprunter que les routes en pointillés, déterminer le chemin qui permet de se rendre le plus rapidement possible du point A au point B.
J'ai donc commencé à calculer les routes en pointillés. Donc pour trouver la longueur de la route qui traverse le rectangle, j'ai commencé par calculer la longueur [BC]. elle mesure 50m ( le théorème de Pythagore le prouve ). Après il faut donc calculer les longueurs [ED] et [BF] mais je ne trouve pas la technique.
Une petite aide serait très gentil. Merci d'avance.
(désolé les pointillés sont fait à l'ordinateur)
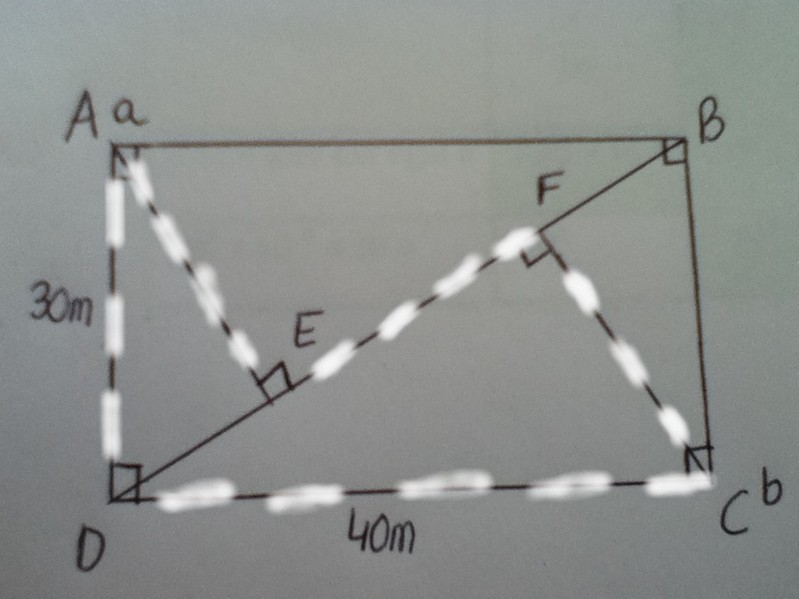
Sachant que l'on ne peut emprunter que les routes en pointillés, déterminer le chemin qui permet de se rendre le plus rapidement possible du point A au point B.
Sur ton dessin il n'y a aucune route en pointillés qui va à B, il est donc impossible de se rendre sur ce point.
j'ai commencé par calculer la longueur [BC]. elle mesure 50m ( le théorème de Pythagore le prouve ).
Sur ton dessin ABCD est codé comme un rectangle ce qui implique que BC = AD
Si le b est inscrit en petit sous le C.
Oui BC=AD. Dans le triangle AED, il me faut au moins deux longueurs pour trouver [DE] donc la longueur pour trouver la longueur [AE] et pour pouvoir appliquer le théorème de Pythagore.
ah oui désolé effectivement c'est une erreur mais j'ai demandé à quelque gens de ma classe qui m'ont dis qu'il fallait utiliser les cocinus des angles...
tu peux déterminer la masure de l'angle grâce aux formules de trigo dans le triangle ABD, puis en déduire la longueur de AE toujours grâce à la trigo mais dans le triangle ADE cette fois.
Juste une proposition, je ne suis pas sûr.
Tu pourrais poser deux équations :
Si tu appelles x la longueur DE qui est égale à FE et y la longueur AE qui est égale à FC,
tu as :
EB^2 = 40^2 - AE^2
(50 - x)^2 = 40^2 - y^2
2500 - 100x + x^2 = 1600 - y^2
900 + x^2 + y^2 = 100x
Or AE^2 + ED^2 = 30^2
y^2 + x^2 = 900
Donc on a si on remplace y^2 + x^2 par 900 dans la première équation :
900 + 900 = 100x
x = 18
900 = y^2 + 18^2
y = 24
Il ne reste plus qu'à calculer ensuite AE + EF + FC = 2y + (50-2x)
Autre proposition
Il existe deux théorèmes
1) Dans un triangle rectangle, le carré d'un côté de l'angle droit est égal au produit de l'hypoténuse par la projection de ce côté sur l'hypoténuse
Ce qui permet de trouver DE : 302 = 50*DE => DE = 18
2) Dans un triangle rectangle le carré de la hauteur relative à l'hypoténuse est égal au produit des segments que cette hauteur détermine sur l'hypoténuse
=> AE2= 18*32 => AE = 24
nous n'avons pas vu ces théorèmes ou alors pas ces techniques.
on a vu Thalès avec les quotients des longueurs d'un triangle
et le théorème de Pythagore : le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.
Tu peux t'en sortir avec Pythagore seulement :
Tu vois que les triangles ADB et BCD sont égaux. Leurs hauteurs AE et FC le sont donc aussi. On appelle la longueur de ces hauteurs y.
De même les triangles ADE et FBC sont égaux. Donc DE = FB. On appelle la longueur de DE et FB x.
Regarde ensuite le triangle AEB. On sait que l'hypoténuse DB fait 50m. Donc EB = 50 - DE = 50 - x. On a :
AB^2 = AE^2 + EB^2
EB^2 = AB^2 - AE^2
(50-x)^2 = 40^2 - y^2
Tu développes et tu obtiens :
2500 - 100x + x^2 = 1600 - y^2
900 + x^2 + y^2 = 100x
Voilà ta première équation.
Regarde maintenant le triangle ADE pour trouver une deuxième équation :
AD^2 = AE^2 + ED^2
30^2 = y^2 + x^2
900 = y^2 + x^2
Du coup, reviens maintenant à la première équation. On avait :
900 + x^2 + y^2 = 100x
Remplace x^2 + y^2 par 900 puisque la deuxième équation nous dit que 900 = y^2 + x^2
On a donc :
900 + 900 = 100x
et donc x = 18
Maintenant, tu peux calculer sans difficulté y :
900 = y^2 + x^2
Donc y = 24
Et le tour est joué :
Le chemin AE, EF et FC vaut :
AE + FC = 2y = 48
EF = DB - (DE + FB) = 50 - 2x = 14
Le chemin AE, EF et FC = 48 + 14 = 62
Or le chemin AD + DC = 30 + 40 donc ...
Dans un triangle rectangle, on a : cosinus(angle) = côté adjacent / hypothénuse
Donc, ici, dans le triangle ABD, on a : cos
donc, dans le triangle ADE, on a : cos

D'après Pythagore :
donc
donc
On fait exactement la même chose dans les triangles BCD et BFC pour trouver FB = 18 et FC = 24
Ensuite : FE = BD - (FB + DE) = 50 - (18 + 18) = 50 - 36 = 14
Pour aller de a à b en suivant les pointilles, on a deux chemins possibles :
- AD + DC = 30 + 40 = 70
- AE + EF + FC = 24 + 14 + 24 = 62
Le deuxième chemin est le plus court
je suis désolé mais je viens de voir que j'ai pas vu les équations et les identités remarquables... désolé mais merci beaucoup quand même... on est en train de voir le chapitre des cocinus donc j'en déduis que l'exercice est sur les cocinus. désolé vous avez du prendre du temps...
MERCI BEAUCOUP ! j'ai tout réussi et j'ai trouvé les mêmes résultats que vous deux dans vos réponses!
Merci à toi Bouli1407 mais aussi à Caracalla qui a du prendre du temps pour répondre même si je n'avais pas trop vu les identités remarquables etc... Mais aussi à Jojo!
Bonne soirée! 


Moi, j'ai un problème, c'est l'année de 4e mais je ne sait pas comment faire l'exercice sachant que je n'ai pas appris le cosinus, mon prof a donné cet exercice en tant que dm. J'aurais besoin d'aide si quelqu'un est connecté  :?
:? :?
:?
Les Formules de Héron peuvent être utile, Merci Internet^^^^ . Il consiste à trouver la longueur de la hauteur.
Bonjour,
avec le nouveau programme l'utilisation des cosinus est un détour inutile pour justifier que deux triangles soient "égaux" ou "semblables" vu que ces nouvelles anciennes notions ont été remises dans le cours.
(avec les anciens programmes, ces notions avaient été supprimées et il fallait faire un détour artificiel par les cosinus)
ancienne méthode par utilisation artificielle du cosinus :
dans le triangle ABD, on a :
dans le triangle ADE, on a :
par conséquent
nouvelle méthode par les triangles semblables :
les triangles rectangles ABD et ADE ayant un angle aigu D égal, ils sont semblables et
(c'est tout de même plus rapide !)
la suite identique au message de Bouli1407
autre variante :
par contre les formules de Heron ??? ... bof la seule que je connais avec ce nom là est celle sur l'aire d'un triangle en fonction se ses côtés, aucun rapport.
alors si maintenant il y en a d'autres ... une invention moderne sans doute donnant à des formules sans nom spécial ce nom nouveau entrainait bien entendu de nouvelles confusions de formules ? pfff ...
si tu as directement dans ton cours la formule donnant la hauteur d'un triangle rectangle ou la relation
sinon la démonstration en est en fait faite au dessus
de toute façon faire un exo ne consiste pas à chercher sur Internet des formules toutes faites exotiques, mais à raisonner et calculer à partir de ce qu'il y a dans ton cours.
le théorème de Pythagore suffit en vrai à faire cet exo, les théorèmes et formules exotiques ne font que raccourcir le calcul de quelques lignes et c'est tout, pas vraiment utile, et surtout si c'est pour utiliser des formules parachutées inconnues.
même les formules
exemple : démonstration de
dans les trois triangles rectangles ADE, ABE et ADB :
le but du jeu est "d'éliminer" AE, AB et BE de ces relations, en tenant compte que
donc déja les deux expressions de AE étant égales :
ensuite on remplace :
on développe (si on ne sait pas développer directement
donc en ajoutant
évidemment le passage par les triangles semblables est bien plus rapide, mais c'est pour montrer que Pythagore et rien que Pythagore suffit.




