Inscription / Connexion Nouveau Sujet
Le triangle podaire
On considère trois points Q, U et V tels que UV=20,5 cm QU=13,5cm VQ=15,5cm
1) Expliquer pourquoi on peut construire le triangle QUV.
2)a. Construire ce triangle.
b. Placer un point P à l'intérieur du triangle QUV.
c. Construire le point Q1 pied de la perpendiculaire menée de P sur (UV)
d. Construire le point U1 pied de la perpendiculaire menée de P sur (QV)
e. Construire le point V1 pied de la perpendiculaire menée de P sur (QU)
DÉFINITION : LE TRIANGLE Q1 U1 V1 EST APPELÉ TRIANGLE PODAIRE DE QUV.
3)a. Démontré que les points Q, U1, P, V1 sont cocycliques.
b. De même pour U, Q1, P, V1 ainsi que V, U1, P Q1.
de l'aide pour le numéro 3 svpp 😑 Je suis bloquée
Bonjour, utilise la propriété qui dit que le cercle circonscrit d'un triangle rectangle a l'hypoténuse pour diamètre (et le milieu de l'hypoténuse pour centre).
Il y a plein de triangles rectangles dans ta figure.
Bonjour à vous deux
Cindy974
Des points cocycliques sont sur un même cercle
Voici une figure qui peut aider
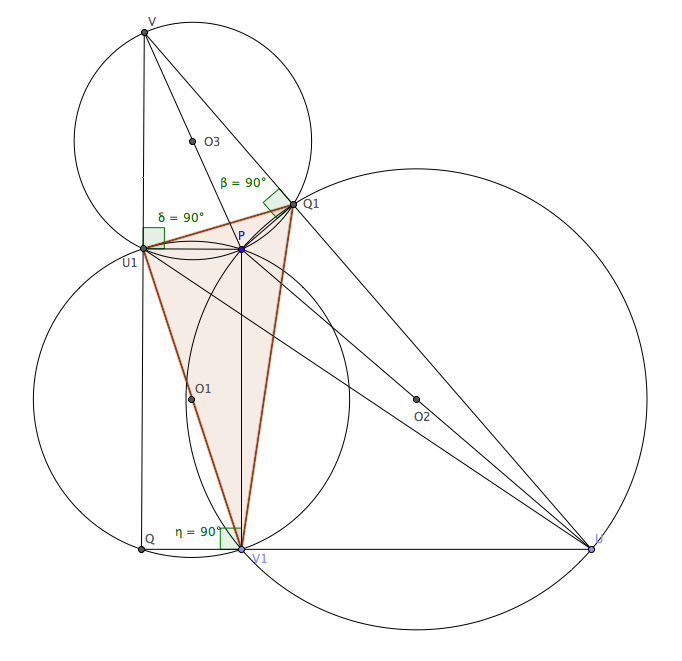
Bonjour,
DÉFINITION : LE TRIANGLE Q1 U1 V1 EST APPELÉ TRIANGLE PODAIRE DE QUV.
C'est le triangle podaire du point P dans le triangle QUV
Pour QUV donné il y a autant de triangles podaires différents que de choix du point P n'importe où.
il n'est donc pas possible de parler du "triangle podaire de QUV" sans préciser pour quel point P !
ceci dit ça ne change rien au problème qui se résout comme dit Glapion
(nota : le triangle QUV n'est pas rectangle, et on s'en fiche,
ni d'ailleurs Q1U1V1 dont la forme dépend du choix du point P)
Bonjour mathafou
Retour en force du grand spécialiste. J'espère que tu as passé de bonnes vacances sans géométrie.
Bonjour mijo
merci, la géométrie en vacance se résumant pour moi surtout à la lecture de cartes 
l'utilisation de la boussole et de l'altimètre, les courbes de niveau etc
je passe pour un vieux crouton à l'ère du GPS sur Smartphone, mais je travaille toujours "à l'ancienne" sans technologie abusive (et inutile dans les coins paumés sans réseau)
toi de même.
pour ce qui est des triangles podaires, il y aurait des tas de choses à dire mais qui dépassent largement le cadre de cet exercice...
en tout cas ici l'usage de Geogebra pour faire varier à volonté le point P est intéressant plutôt qu'une figure statique.
on peut ainsi chercher les positions de P pour lesquelles le triangle podaire a une forme remarquable...
mathafou
C'est un domaine qui ne m'est guère familier, quand j'étais plus jeune mon loisir préféré était la planche à voile en lac et en mer.
Je n'avais aucun souvenir concernant les triangles podaires. J'essaierai avec Geogebra de faire varier le point P, c'est un problème intéressant.
Je ne suis pas parti en vacances depuis plusieurs années et dimanche dernier j'ai fait une chute dans l'escalier en béton d'accès à ma maison et me suis cassé une côte. Maintenant repos forcé pour au moins 2 semaines.
Depuis le 22-08-19 à 11:15 Cindy974 n'a pas donné signe de vie, encore un qui attendait sans doute que l'on fasse l'exercice à sa place.


