Inscription / Connexion Nouveau Sujet
Lemniscate de bernouilli
Bonjour,
j'ai fait un exo et j'aimerai avoir confirmation que celui ci est juste.
Enoncé : On considère les points F(1,0) et F'(-1,0).
Déterminer une équation polaire de l'ensemble C des points M du plan tels que MF.MF' = 1. Etudier et tracer cette courbe
Alors je pose M(x,y)
on a donc : (x-1)*(x+1) +y^2 = 1
ce qui est l'equation d'un cercle de centre O et de rayon racine de 2.
L'equation polaire d'un tel cercle est donc :
 ^2 = 2*cos(2
^2 = 2*cos(2 )
)
Est-ce juste ?
Car mon exo est intitulé "lemniscate de bernouilli) et quand je cherche sur des sites de maths, la courbe n'est pas un cercle, et ressemble a un signe  .
.
Merci d'avance pour votre aide
bernoulli et pas Bernouilli
F(1,0) et F'(-1,0).
M(x,y)
MF² = (x-1)² + y²
MF'² = (x+1)² + y²
MF.MF' = 1.
MF².MF²' = 1² = 1
[(x-1)² + y²].[(x+1)² + y²] = 1
(x²-2x+1+y²)(x²+2x+1+y²)=1
x^4 + 2x³+x²+x²y²-2x³-4x²-2x-2xy²+x²+2x+1+y²-x²y²+2xy²+y²+y^4 = 1
x^4 - 2x² + 2y² + y^4 = 0
(x² - 1)² - 1 + (y² + 1)² - 1 = 0
(x² - 1)² + (y² + 1)² = 2
En polaire:
x = r.cos(theta)
y = r.sin(theta)
(r².cos²(theta) - 1)² + (r².sin²(theta) - 1)² = 2
r^4.cos^4(theta) - 2r².cos²(theta) + 1 + r^4.sin^4(theta) - 2r².sin²(theta) + 1 = 2
r^4.(cos^4(theta) + sin^4(theta)) - 2r².(cos²(theta) + sin²(theta)) = 0
r^4.(cos^4(theta) + sin^4(theta)) - 2r² = 0
r = 0 convient.
Si r est différent de 0:
r².(cos^4(theta) + sin^4(theta)) = 2
r = +/- V[2/(cos^4(theta) + sin^4(theta))]
-----
Sauf distraction. 
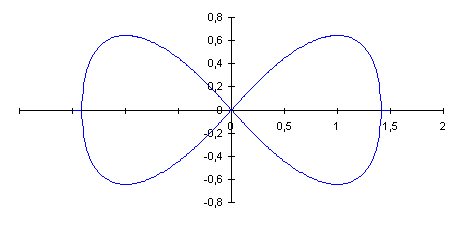
C'est donc qu'il doit y avoir une erreur quelque part!
Tu as écrit que le produit scalaire des vecteurs MF et MF' était égal à 1, alors que je crois que c'est le produit des modules qu'il faut prendre...
en élevant au carré ((x-1)^2+y^2)((x+1)^2+y^2)=1
En polaire (p,t) (p^2-2pcost+1)(p^2+2pcost+1)=(p^2+1)^2-4p^2(cost)^2=1
p^2(p^2+2(1-2(cost)^2))=0 ou encore p^2(p^2-2cos2t)=0
soit le point p=0 et la lemniscate p^2=2cos2t
C'est bien l'équation que tu avais trouvée, mais je ne sais pas comment tu y étais arrivé, et en tout cas ce n'est pas un cercle! ( un cercle de centre O c'est p=a, un cercle passant par O et centré sur l'axe des x c'est p=acost)
Correction de ma réponse précédente: (erreurs de signe).
F(1,0) et F'(-1,0).
M(x,y)
MF² = (x-1)² + y²
MF'² = (x+1)² + y²
MF.MF' = 1.
MF².MF²' = 1² = 1
[(x-1)² + y²].[(x+1)² + y²] = 1
(x²-2x+1+y²)(x²+2x+1+y²)=1
x^4 + 2x³+x²+x²y²-2x³-4x²-2x-2xy²+x²+2x+1+y²+x²y²+2xy²+y²+y^4 = 1
x^4 - 2x²+ 2x²y² + 2y² + y^4 = 0
En polaire:
x = r.cos(theta)
y = r.sin(theta)
r^4.cos^4(theta) - 2.r².cos²(theta) + 2.r².cos²(theta).r².sin²(theta) + 2r².sin²(theta) + r^4.sin^4(theta) = 0
r^4.cos^4(theta) - 2.r².cos²(theta) + 2.r^4.cos²(theta).sin²(theta) + 2r².sin²(theta) + r^4.sin^4(theta) = 0
r^4.cos^4(theta) - 2.r².cos²(theta) + 2.r^4.cos²(theta).sin²(theta) + 2r².sin²(theta) + r^4.sin^4(theta) = 0
r = 0 est solution.
Si r est différent de 0 -->
r².cos^4(theta) - 2.cos²(theta) + 2.r².cos²(theta).sin²(theta) + 2.sin²(theta) + r².sin^4(theta) = 0
r²(cos^4(theta) + 2.cos²(theta).sin²(theta) + sin^4(theta)) = 2.cos²(theta) - 2.sin²(theta)
r²(cos²(theta) + sin²(theta))² = 2.(cos²(theta) - sin²(theta))
r² = 2.(cos²(theta) - sin²(theta))
r² = 2.cos(2.theta)
-----
Sauf nouvelle distraction. 


 géométrie en post-bac
géométrie en post-bac