Si A et B ont des coord. entières =>
* AB est entier
* xD=xA entier et xB=xC entier

Comme ABCD est un carré AB=AD=BC
donc AD et BC sont entiers

yD=yA+AD entier
yC=yB+BC entier

Il y a peut-être plus rapide...

Philoux

A(a ; b)
B(c ; d)

avec a, b, c et d entiers.

On a C(X ; Y) avec X et Y à trouver.

vecteur(AB) = (c-a ; d-b)
vecteur(BC) = (X-c ; Y-d)

AB et AC sont perpendiculaires -->  vecteur(AB) . vecteur(BC) = 0, on a donc:

(c-a).(X-c) + (d-b).(Y-d) = 0  (1)

|AB|² = (c-a)² + (d-b)²
|BC|² = (X-c)² + (Y-d)²

On a |AB| = |BC| et donc aussi |AB|² = |BC|²
-->
(c-a)² + (d-b)² =  (X-c)² + (Y-d)²   (2)

On a le système:
(c-a).(X-c) + (d-b).(Y-d) = 0
(c-a)² + (d-b)² =  (X-c)² + (Y-d)²

Résoudre ce système donne X et Y en fonction de a, b, c et d qui sont connus.

(c-a).(X-c) + (d-b).(Y-d) = 0
(X-c) = -(d-b).(Y-d)/(c-a)

(c-a)² + (d-b)² = ( -(d-b).(Y-d)/(c-a) )² + (Y-d)²

(c-a)² + (d-b)² = (d-b)².(Y-d)²/(c-a)² + (Y-d)²

(c-a)² + (d-b)² =  (Y-d)² (1 + (d-b)²/(c-a)²)

(c-a)² + (d-b)² =  (Y-d)² ((c-a)² + (d-b)²)/(c-a)²

(Y - d)² = (c-a)²

Y - d = (+/-)(c-a)

Y = d +/- (c-a) et donc Y est entier.

(X-c) = -(d-b).(Y-d)/(c-a)

(X-c) = -(d-b).(d +/- (c-a)-d)/(c-a)

(X-c) = -(d-b).(+/- (c-a))/(c-a)

(X-c) = -/+(d-b)

X = c -/+ (d-b) et donc X est entier.

C a donc des coordonnées entières.
-----
Même démo pour D.

Sauf distraction.  

Attention,

Mon raisonnement est faux (distances entières !) et incomplet : j'ai pris AB parallèle à Ox

En raisonnant avec les affixes en disant BC ortho AB => zBC=izAB

c'est plus rapide et juste surtout

Philoux

oups

merci J-P

Philoux

En affixes complexes, si les sommets sont ABCD dans le sens trigonométrique,
(zC-zB)=i(zB-zA) donc zC=(1+i)zB-izA donc si A et B sont à coordonnées entières (les affixes sont des entiers de Gauss, qui ont structure d'anneau), C également.
de même pour D, à partir de (zD-zC)=i(zC-zB)

Je développe un peu plus

A : zA à coord. entières zA=a+ia'
B : zB à coord. entières zB=b+ib'

ABCD carré =>
AB _|_ BC => (zC-zB)=i(zB-zA) => zC=zB+i(zB-zA)=b+ib'+i(b-a+i(b'-a'))= b-b'+a'+i(b'+b-a) => C a des coord. entières

AB _|_ AD => (zD-zA)=i(zB-zA) => zD=zA+i(zB-zA)=a+ia'+i(b-a+i(b'-a'))= a+a'-b'+i(a'+b-a) => D a des coord. entières

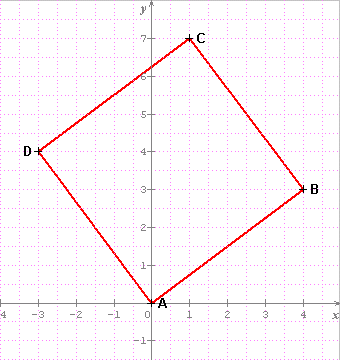
exemple ci-dessous avec A(0,0) et B(4,3)

Philoux

Bonjour;
(*)Soient et les affixes repectifs des points et .
est un carré donc (resp ) est l'image de (resp ) dans la rotation de centre (resp ) et d'angle ce qui s'écrit:

ce qui montre bien que les parties réelles et imaginaires de et sont entières vu que celles de et le sont.
Sauf erreur bien entendu