Inscription / Connexion Nouveau Sujet
Oui exactement et je dois aussi remettre toutes les idées en ordre et le rédiger, ça me permettre déjà de vérifier une première fois!
Je me pose une question, comment peut-on justifier que M a pour coordonnées (2-x²,2-x²)? Pour l'ordonnée, c'est parce qu'il a la même que M qui appartient à Cv mais pour l'abscisse, je ne vois pas pourquoi c'est 2-x²?
Voici ce que donne l'exercice après que je l'ai refait: Je ne joint pas les figures de Geogebra qui sont similaires bien sûr à ceux déjà mis au début!
==CONJECTURER==
1. Figure réalisée sur Geogebra
2. Le lieu décrit par le point P quand M décrit (Cv) formerait un demi-cercle de centre O(0,0), qui est l'origine du repère.
==JUSTIFIER MATHÉMATIQUEMENT==
3.a) La construction de K est possible pour x>=0 puisque K
(Cu) défini par u(x)=
x sur [0;+
].
3.b) H a pour coordonnées (2-x²,2-x²) ayant la même ordonnée que M (de coordonnées (x,2-x²) car M(Cv)) et d'abscisse 2-x² car yH=yM et comme H(d), xH=yH.
K a pour coordonnées (2-x²,2-x²) car K a la même abscisse que H (de coordonnées (2-x²,2-x²) et K(Cu) (avec u fonction définie par u(x)=x), d'où yk=f(xK), donc yK=2-x².
P a pour coordonnées (x,2-x²) car MHKP est un rectangle et (KP)
(x0), donc xP=xM et yP=yK.
4.a) xP²+yP²=2P. P cercle de centre l'origine du repère, de coordonnées (0,0) et de rayon 2 et puisque yP>0, P la partie supérieure du demi-cercle du cercle de centre l'origine et de rayon 2 et yP=2-x². Donc h(x)=2-x²
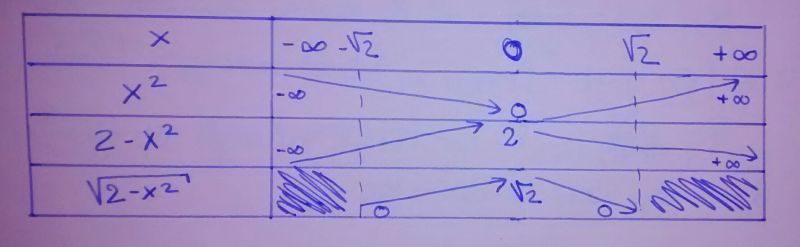
4.b) Pour le tableau de variation, voir la photo ci-jointe.
4.c) Courbe représentative de h (y=2-x²) tracée sur Geogebra
4.d) Pour la distance OP, vu que OP est le rayon du demi-cercle considéré, OP=(xP-xO)²+(yP+yO)²
4.e) Enfin, cette étude nous a permis de déterminer que le lieu décrit par le point P lorsque M décrit (Cv) est la représentation de la fonction h (y=2-x²). Ce lieu forme un demi-cercle de rayon constant (OP) et de centre l'origine du repère.
Est-ce que tout ceci est correct? 
Vérifiez quand vous avez le temps, je ne suis pas pressé! Et encore une fois, merci pour votre aide qui m'est précieuse 
Annuler
connectez vous