Inscription / Connexion Nouveau Sujet
Lieu d'un point avec Geogebra et étude d'une fonction
Bonjour,
J'ai ici un exercice que j'arrive pas à faire, en effet je suis bloqué dès les premières questions avec Geogebra... Merci pour l'aide que vous m'apporterez!
L'exercice est le suivant:
"On a une fonction u définie sur [0 ; + [ par u(x)=
[ par u(x)= x puis une seconde fonction dénommée v, définie sur
x puis une seconde fonction dénommée v, définie sur  par v(x)= 2-x².
par v(x)= 2-x².
Ensuite, dans un repère orthonormé ayant O pour origine, on doit construire les courbes représentatives de ces fonctions, respectivement nommées (Cu) et (Cv) et aussi la droite d ayant pour équation y=x.
Après, nous avons le point M de la courbe (Cv) d'abscisse x et aussi le point H de la droite d d'ordonée analogue au point M. Quand la construction est possible, on note le point K, point de (Cu) qui est d'abscisse identique à celle de H, enfin, on note P le point tel que KPMH soit un rectangle.
On peut ensuite déterminer le lieu décrit par le point P lorsque M décrit (Cv).
Questions:
1) Construire la figure avec Geogebra (Rappel: x=sqrt(x))
x=sqrt(x))
2) Utiliser l'outil Lieu pour conjecturer le lieu que décrit P quand M décrit la courbe (Cv)
3)a. Pour quelles valeurs dex, peut-on construire K?
b. Exprimer les coordonnées de H, puis de K et de P en fonction de x
2)a.A partir des coordonnées précédentes de P, déduire que P appartient à la courbe représentative d'une fonction h et la définir.
b. Dresser le tableau de variation de cette fonction en utilisant les études conjointes
c. Tracer la courbe représentant fonction h sur Geogebra
d. Calculer OP
e. Conclure"
Et je suis bloqué dès la première question pour la figure, je ne vois pas quand est-ce que le point K peut ne pas exister notamment?
Bonjour,
Essaye de bouger M sur la courbe, tu verras que si M passe sous l'axe des x alors K n'existe plus.
Est-ce qu'il y a quelque chose que tu n'ais pas arrivé à construire ?
Voilà ce que j'obtiens quand je fais la figure, je vois qu'il y a un problème, notamment avec le lieu de P mais je ne sais pas où...? Notamment dans ma figure, K ne disparaît jamais en fait!
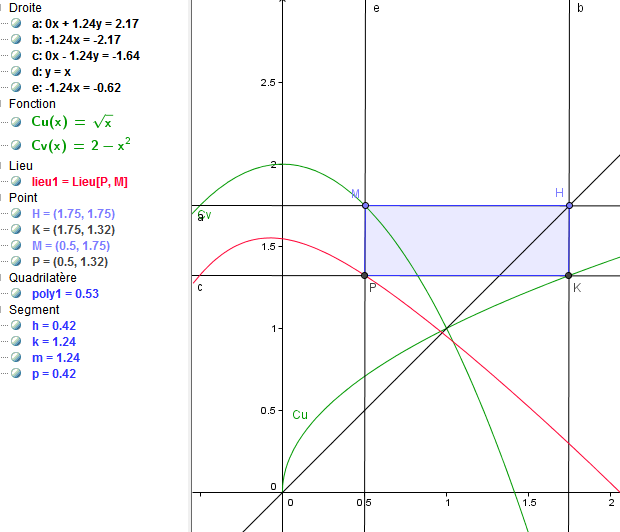
En effet, REMYK, comme K est de même ordonnée de P et que P n'existe que pour x>0, si H est <0, K ne peut exister!
Pour former le lieu, vous êtes censé(e) fabriquer un CURSEUR a, et faire dépendre les Coordonnées de M, de P et de K de la valeur de ce Curseur; (Par Exemple, M=(a;2-a^2)); Ensuite vous construisez le Point P, et Appliquez l'outil Lieu sur P et Le Curseur.... Regardez alors si vous trouvez un Lieu plus proche de celui proposé par Glapion ....
Comment puis-je faire dépendre chaque point d'un curseur tout en ajoutant les conditions d'appartenance à la courbe.. par exemple?
(Par Exemple, M=(a;2-a^2))
Avec une virgule plutôt, Dans la Barre de Saisie .....
Et Dans ce cas, M appartient à Cv puisque yM=v(xM)
Pas forcement besoin d'un curseur. Tu poses M sur Cv avec l'outil "Point sur Objet"
si tu construis tous les points H;K;P en utilisant M, quand M bougera tous les autres bougeront et quand tu utiliseras le bouton Lieu en désignant P puis M, il dessinera le lieu de P (qui ressemble visiblement à un cercle sur mon dessin).
Oui en effet c'est ce que j'avais fait Glapion, avec des perpendiculaires pour former un rectangle!
Mais je vais aussi essayer avec le curseur...
Je ne comprends pas... En faisant la méthode de Glapion je ne parviens pas à avoir ce qui est attendu, je refais comme au départ à chaque fois!
Passons au curseur...
Oui ça marche aussi bien sûr. Mais comme le dit REMYK, il faut taper les formules
(attention, pas avec des ; qui sont pour les coordonnées polaires mais M=(a,2-a^2))
J'ai réussi le curseur pour M! Par contre, j'en fais aussi un pour H, un pour K...? Ou par exemple pour H, je le place juste sur la droite d?
ha non, H; K; P il faut les construire avec des parallèles ou des perpendiculaires. Si tu crées de nouveaux curseurs, ils ne dépendront pas de M.
Ah d'accord! J'ai fait le rectangle avec les perpendiculaires et des parallèles et j'ai toujours le même problème... Je pense que c'est parce que mon point H reste fixe, contrairement aux autres points mais je ne sais pas pourquoi?
H ne peut pas être fixe. Construis le en faisant l'intersection de la parallèle menée de M à l'axe ox avec la droite y=x
En effet, ça fonctionne enfin avec les deux méthodes!! 
Donc, pour la question 2, le lieu que décrit le point P quand M décrit (Cv) est un demi-cercle dont le diamètre a pour abscisse x=0?
Question 3, la construction de K est possible lorsque x>0, mais comment puis-je le justifier?
Un demi-Cercle Dont Le CENTRE a pour abscisse x=0 (et pour ordonnée y=0....);
Pour la Construction de K, vous pourriez relire les Posts Plus hauts ....
Oui d'accord pour le demi-cerlce, et pour K, j'avais en effet écrit "K est de même ordonnée de P et que P n'existe que pour x>0, si H est <0, K ne peut exister!".
Ensuite, pour les coordonnées de H, ça donne (2-x²,2-x²), par contre je ne vois pas comment on a celles de P et K?
L'Abscisse de K y est identique à celle de H et pour son Ordonnée, K appartient à Cu ....
Par contre, P est trouvé avec l'Intersection de 2 Droites Perpendiculaires....
Donc on a K(2-x², √x) mais je ne vois pas comment avoir P...? On peut avec l'intersection de deux droites perpendiculaires ?
NON; K appartient à Cu; yK=f(xK); xK=2-x^2; Donc, Ici, yK= sqrt(2-x^2);
Pour P, il est ici l'intersection de la perpendiculaire à (HK) passant par K, et de la parallèle à (HK) passant par M;
Ah oui en effet!... Et pour P, je prends les équations de la perpendiculaire et de la parallèle? Je ne comprends pas comment je peux faire...
Non, pour P, après avoir placé M, H et K avec le logiciel, vous Tracez vraiment la parallèle et la perpendiculaire avec le logiciel, et vous placez P à leur intersection;
Oui, ça je suis d'accord et je l'ai fait mais comment puis démontrer les coordonnés de P, que je dois déterminer dans la question 3)b.?
Ah, OK, Désolé....
Vous pourriez Regarder le Sch"ma et vous apercevoir que P est de même abscisse que M et de même ordonnée que K ...
Et pour le justifier, j'indique que c'est un rectangle et avec les perpendiculaires, c'est de même abscisse / ordonnée que tel point et donc on a P(2-a²,√2-a²)
Schéma*....
Parce que MHKP est un RECTANGLE ET que (KP) est parallèle à l'axe des abscisses (ce n'est pas un rectangle "incliné."..);
Vous pourriez aussi Raisonner en termes de Coefficients Directeurs, de Droites perpendiculaires et d'intersections ....
En effet, il y a plein de possibilités! Et ensuite, pour la question 4, pour trouver l'équation de h à partir de P, comment peut-on le faire? :/
P a ici la même abscisse que M et la même ordonnée que K; P(a; sqrt(2-a^2));
xP ^ 2 + yP^2 = 2 P appartient à un cercle de Centre l'origine et de rayon sqrt(2), et, puisque yP>0, alors P appartient au demi-cercle supérieur de ce cercle; (Plus précisément, yP=sqrt(2-x^2), demi-cercle de centre l'origine et de rayon sqrt(2))...
De quelle Droite ???? Vous avez l'impression que P décrit une Droite ?????
yP=sqrt(2-x^2), demi-cercle de centre l'origine et de rayon sqrt(2)
h(x)=sqrt(2-x^2) .....
Citation :
yP=sqrt(2-x^2), demi-cercle de centre l'origine et de rayon sqrt(2)
;
h(x)=sqrt(2-x^2) .....
yP=sqrt(2-x^2), demi-cercle de centre l'origine et de rayon sqrt(2)
;
h(x)=sqrt(2-x^2) .....
Oui en effet...
Et cela correspond parfaitement !
Pour le tableau de variation, ça devrait aller, et pour calculer OP, j'utilise les coordonnées et je fais (xP-xO,yP-yO)?
Oui! Et pour conclure l'étude, que devons-nous dire? Que le fonction h décrit le lieu de P?... Ou que le lieu forme un demi-cercle?
Le fait que le lieu de P y est la Représentation Graphique de h est indiqué dans l'énoncé; Par contre Le fait que le lieu forme un demi-cercle, (Rayon Constant) pourrait aussi être une Conclusion de cet Exercice, parce qu'il n'était pas évident que vous l'ayez vu dans la question c. ....
Le fait que le lieu forme un demi-cercle, (Rayon Constant) pourrait aussi être une Conclusion de cet Exercice, parce qu'il n'était pas évident que vous l'ayez vu dans la question c. ....
Cela rejoint bien entendu le fait que :
OP reste constante, ne dépend pas de l'abscisse x de M
Oui tout à fait c'est ce que je pensais en effet :=) Je vous remercie de votre aide et du temps passé à me répondre! 

 ...
...
