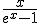Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

lim x/exp(x)-1

Posté par
Antenne 23-10-14 à 11:38

Bonjour,

On me demande dans mon DM de déterminer la limite de f(x)= x/exp(x)-1 en - ∞.

Je trouve une FI car "0/0".

Je sais qu'il faut changer de forme f(x) mais je bloque...
merci de votre aide.

Antoine

Posté par
cauchy77re : lim x/exp(x)-1 23-10-14 à 11:39

bonjour,

possible de mettre des parenthèses SVP?

on ne peut pas deviner l'expression de f sans elles...

Posté par
Antennere : lim x/exp(x)-1 23-10-14 à 11:45

voila

lim x/exp(x)-1

Posté par
cauchy77re : lim x/exp(x)-1 23-10-14 à 11:49

Ah c'est mieux ainsi!

pour ta gouverne, il n'y a aucune  F.I.  car le numérateur tend vers  -\infty  et le dénominateur vers -1

je ne sais pas comment tu t'y es pris mais il n'y a aucun calcul supplémentaire!

Posté par
Antennere : lim x/exp(x)-1 23-10-14 à 11:54

oui en effet, je me suis trompé lorsque j'ai écrit l'énoncé... On me demande de déterminer la limite en 0.
Je ne sais pas ce qu'il m'est passé par la tête...

Posté par
cauchy77re : lim x/exp(x)-1 23-10-14 à 12:06

Ah  ça  change  tout  là!

regarde  comment  procéder  :

on  cherche  \lim_{x\to 0} {\frac{x}{e^x - 1}

voyons  ce  que  donne  la  limite  inverse :

\lim_{x\to 0} {\frac{e^x - 1}{x} = \lim_{x\to 0} {\frac{e^x - e^0}{x - 0}

et  on  reconnait  là  le  taux  d'acroissement  de  la  fonction  exponentielle  en  0,  càd  que  :

\lim_{x\to 0} {\frac{e^x - e^0}{x - 0} = (e^x)'(0) = e^0 = 1

donc  \lim_{x\to 0} {\frac{x}{e^x - 1} = 1

Posté par
Antennere : lim x/exp(x)-1 23-10-14 à 12:12

j'ai compris, je me doutais qu'il fallait trouver la limite inverse.
merci beaucoup

Posté par
Antennere : lim x/exp(x)-1 23-10-14 à 12:19

Je peux utiliser le même procéder pour trouver la limite en +∞ ?

Posté par
Glapion Moderateurre : lim x/exp(x)-1 23-10-14 à 12:46

Quel procédé ? celui du taux d'accroissement ? ben non.

Posté par
cauchy77re : lim x/exp(x)-1 23-10-14 à 13:00

Non car un taux d'accroissement se calcule en une valeur finie, donc il faut chercher autrement pour la limite en  +\infty


Rechercher
Menu
Espace membre
15 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !