Niveau terminale

Limite d'une suite récurrente

Posté par
meso15 03-01-21 à 20:59

Bonjour à tous,
Tout d'abord, je vous souhaite une bonne année !

J'ai un DM de maths pour******et j'aimerais que vous jetiez un coup d'?il sur le premier exercice.
Voici l'énoncé
Quel sens donner à l'écriture infinie $\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{...}}}}$ ?
Une possibilité est de voir cette écriture comme la limite d'une suite d'écritures finies.
$\sqrt{1} \rightarrow \sqrt{1+\sqrt{1}} \rightarrow \sqrt{1+\sqrt{1+\sqrt{1}}} \rightarrow ...$

Pour passer d'une écriture E à la suivante on écrit $\sqrt{1+E}$
puis on met le tout sous la racine.
Chaque écriture représente un nombre et si la suite de ces nombres converge vers une limite l alors on pourra dire $\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{...}}}}= l$

On définit donc la suite $(U_{n})_{n\in N}$ par $\begin{cases} & u_{0}=1 \\ & u_{n+1}=\sqrt{1+u_{n}} \end{cases}$

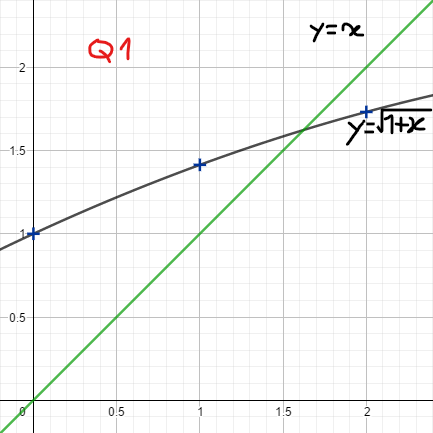
1) Sur un même graphique représenter les courbes d'équation $y=x$
et $y=\sqrt{1+x}$ pour $x$ dans l'intervalle $[ 0 ; 2 ]$
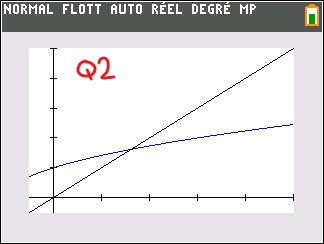
2) Construire graphiquement les premiers termes de la suite et conjecturer le comportement de la suite.
3) Démontrer par récurrence que pour tout entier naturel $n$ on a $1\leq u_{n}\leq u_{n+1}\leq 2$
4) Justifier que la suite converge et calculer sa limite.

Et voilà mes réponses:
1) Voir pièce jointe graphe Q1
2) Voir pièce jointe graphe Q2
Conjecture : La suite semble être croissante et majorée par M=2 à partir d'un certain rang donc elle semble être conergente.
3) On identifie la fonction $f$ telle que : $u_{n+1}=f(u_{n})$ :
$f(x)=\sqrt{1+x}$
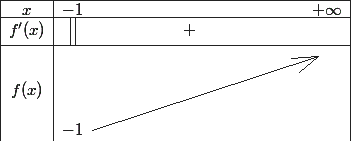
On étudie les variations de la fonction $f$ .
Calcul de la derivée $f'$ :
$f(x)=\sqrt{1+x}$ donc $f'(x)=\frac{1}{2\sqrt{1+x}}$
$f(x)=\sqrt{1+x}$ est définie sur $\left[-1 \right;+ \infty [$ et sa dérivée est définie sur $\left[0 \right;+ \infty [$ car $f'(x)>0$ pour tout $x>-1$
*tableau de variations en pj*
$f(-1)=\sqrt{1-1}=0$
Démonstration par récurrence de $P(n):1\leq u_{n}\leq u_{n+1}\leq 2$
Initialisation:
Pour $n=0$ on a:
$u_{0}=1$ et $u_{1}=\sqrt{1+u_{0}}=\sqrt{1+1}=\sqrt{2}$
On a bien $1\leq u_{0}\leq u_{1}\leq 2$ donc $P(0)$ est vraie.
Hérédité:
Soit un entier naturel n. Supposons que $P(n)$ est vraie et montrons que $P(n+1)$ est vraie.
$1\leq u_{n}\leq u_{n+1}\leq 2\\ \Leftrightarrow f(1)\leq f(u_{n})\leq f(u_{n+1})\leq f(2)\\ \Leftrightarrow 1\leq \sqrt{2}\leq u_{n+1}\leq u_{n+2}\leq \sqrt{3}\leq 2$
Donc $P(n+1)$ est vraie.
Conclusion:
$P(0)$ est vraie et $P(n)$ est héréditaire à partir du rang $0$
, donc par récurrence $P(n)$ est vraie pour tout entier naturel $n$ .

4) D'après la question 3) la suite est croissante et majorée par $M=2$
donc $(u_{n})$ converge vers un réel $l$ tel que $1\leq l\leq M$

Calcul de la limite $l$ :
$f$ est une fonction continue et la suite $(u_{n})$ est définie par $u_{n+1}=f(u_{n})$ et elle converge vers un réel $l$ donc $l$ vérifie l'équation : $l=f(l)$
Comme $u_{n+1}=\sqrt{1+u_{n}}$ alors on a $l=\sqrt{1+l}$
$l=\sqrt{1+l} \\\Leftrightarrow l^{2}=1+l \\\Leftrightarrow l^{2}-(1+l)=0 \\\Leftrightarrow l^{2}-1-l=0$
$l^{2}-1-l=0$ est une équation polynôme du second degré donc on résoud l'équation en cherchant les racines.
$\Delta = b^{2}-4ac \\\; \; \; \:= (-1)^{2}-4\times 1\times (-1) \\\; \; \; \:=5$
$\Delta > 0$ donc il existe deux racines.
$l_{1}=\frac{-b-\sqrt{\Delta }}{2a} = \frac{1-\sqrt{5 }}{2}$
$l_{2}=\frac{-b+\sqrt{\Delta }}{2a} = \frac{1+\sqrt{5 }}{2}$
Donc la limite $l$ est égale à $l_{1}$ ou à $l_{2}$ sauf qu'on travaille sur l'intervalle $[\; 0\; ; \; +\infty \; [$ et $l_{1}= \frac{1-\sqrt{5 }}{2} \simeq -0,62$ donc la limie $l=\frac{1+\sqrt{5 }}{2} \simeq 1,62$
Donc la suite $(u_{n})$ converge vers $\frac{1+\sqrt{5 }}{2}$ . $Limite d\'une suite récurrente$
$\lim_{n\rightarrow +\infty } (u_{n})= \frac{1+\sqrt{5 }}{2}$ .

Merci d'avance,

_{*modération > meso15, pour la gestion du temps, cela dépendra essentiellement de ton investissement sur le sujet*}

Posté par re : Limite d'une suite récurrente 03-01-21 à 21:01

Pour question 1 et 2

$Limite d\'une suite récurrente$

$Limite d\'une suite récurrente$

Posté par re : Limite d'une suite récurrente 04-01-21 à 11:16

Bonjour,
Q1: Ok
Q2: Ton graphique n'indique pas grand chose. Pourquoi "M=2"?
Q3: Le début de ta réponse ne correspond pas à la question posée. L'étude de f(x) pourrait en revanche être inclue dans la Q1. En ce qui concerne la récurrence, ça me parait bon.
Q4: Pourquoi 2?

Posté par re : Limite d'une suite récurrente 04-01-21 à 11:17

Ok pour le calcul de la limite

Posté par re : Limite d'une suite récurrente 04-01-21 à 12:08

Bonjour à vous deux,
juste pour rappeler à meso15 le principe de visualisation des suites récurrentes.
_{tu as la méthode expliquée là si tu veux

tu dessines la courbe (ici y=(x+1)) et la droite y=x qui sert à rabattre les points de l'axe des y sur l'axe des x pour pouvoir continuer la récurrence. Les segments semblent rebondir un coup sur la courbe et un coup sur la droite; A chaque verticale bleue, il y a un terme de la suite.}
ça donne :
$Limite d\'une suite récurrente$
on voit bien les termes de la suite converger et ça permet aussi de vérifier la valeur que tu as trouvée pour la limite.

Posté par re : Limite d'une suite récurrente 05-01-21 à 22:57

sanantonio312
Merci de m'avoir répondu !
Pour question 2, je pense que j'ai écrit M=2 après avoir fait question 3. Du coup faut-il conjecturer que la suite converge seulement ?
Pour question 3, j'ai commencé par l'étude de f(x) pour pouvoir démontrer par récurrence et donc pouvoir remplacer u_n et u_n+1 par f(u_n) et f(u_n+1).
Pour question 4, là encore j'ai mis M=2 car j'ai démontré dans la question 3 que tous les termes de la suite sont compris entre 1 et 2

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Suites en terminale
8 fiches de mathématiques sur "Suites" en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Limite d'une suite récurrente

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths