Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

limite de exp

Posté par
rimo 16-02-13 à 22:12

Hello, please help me in this exercise it's so important for me.
Thank you

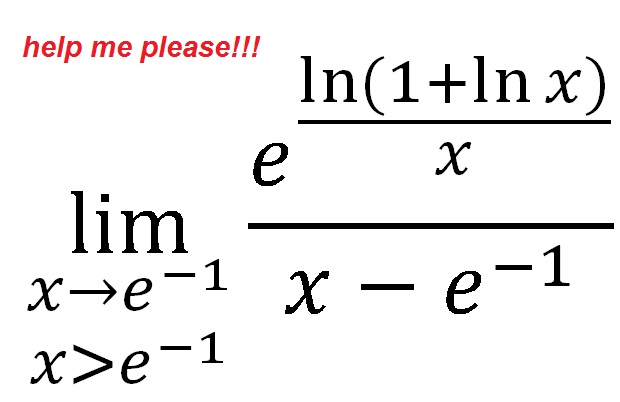
limite de exp

Posté par
Nicolas_75 Correcteurre : limite de exp 17-02-13 à 00:00

Bonjour,

En posant x=e^{-1}+h, on s'intéresse à la limite en 0+ de \frac{ e^{ \frac{\ln\left( 1+\ln\left(e^{-1}+h\right) \right)}{e^{-1}+h} } }{ h }

Cette expression est égale à :
\frac{ e^{ \frac{\ln\left( \ln(1+eh) \right)}{e^{-1}+h} } }{ h } = \frac{ \left( e^{ \ln\left( \ln(1+eh) \right) } \right)^{\frac{1}{e^{-1}+h}}}{ h } = \frac{ \left( \ln(1+eh) \right)^{\frac{1}{e^{-1}+h}}}{ h }

= \left( \frac{ \ln(1+eh) }{ h }\right)^{\frac{1}{e^{-1}+h}} \times \left(\frac{1}{h}\right)^{1-\frac{1}{e^{-1}+h}}

Le premier facteur tend vers e^e, et le second vers 0.

Sauf erreur !

Nicolas

Posté par
rimolimite exp 17-02-13 à 14:37

thank you so mush my teatcher, you are great


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !