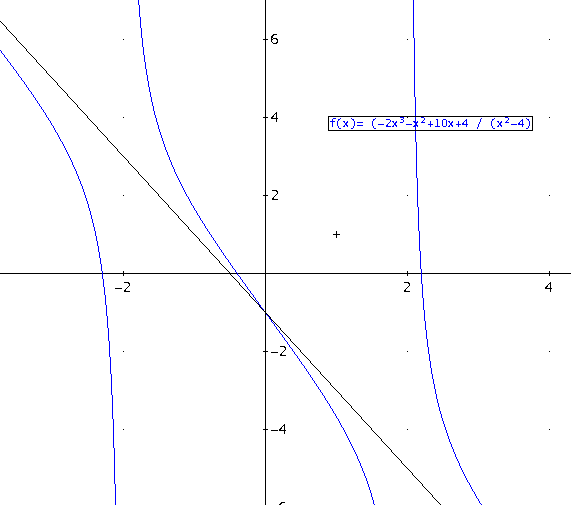Inscription / Connexion Nouveau Sujet
Limites : Asymptotes + Quelques fonction (dérivés et variations)
Bonjour
Je suis nouvelle sur ce forum et j'aurais besoin d'aide pour mon DM de maths.
J'ai essayer de commencer l'exercice mais je n'arrive pas à aller plus loin que la deuxième question et en plus je ne sais même
pas si ce que j'ai fait pour la première et la deuxième question est juste ! = S
Voici L'exercice :
On considère la fonction f définie par f(x)= -2x3-x2+10x+4 / x2-4
1°) Déterminer 4 réels a, b, c et d tels que f(x) = ax + b + ( c / x-2 ) + ( d / x+2 )
J'ai trouvé comme résultats : a= -2 b= -1 c= -2 d= 4
2°)Etudier les variations de la fonction f et donner son tableau de variation
J'ai donc calculer la dérivé et j'ai obtenu f'(x)= 2x4-14x2+40 / (x2-4)2 et j'en ai déduit que la fonction était croissante
Mais je n'arrive pas a continuer, car je n'ai pas du tout compris le cours pour les asymptotes.
3°)On désigne par Cf la courbe représentative de f.
a) préciser les asymptotes de Vf parallèles aux axes de coordonnées.
b) montrer que la droite (D) d'équation y=-2x-1 est une asymptote oblique de Cf.
c) Préciser la position de Cf par rapport à (D).
4°) Montrer que I(0;-1) est un centre de symétrie de Cf
5°) Donner une équation de la tangente (T) à Cf au point I
Voila ! Merci D'avance ! 
Bonjour
1) je dirai a= -2 b= -1 ok mais c= 1 et d= 1
2AV x=2 et x=-2
1AO y = -2x-1
Je crois qu'il y a 1 signe - devant la dérivée
A toi
A+
oui effectivement, deux valeurs interdites et une dérivée négative donc tu peut tracer ton tableau de variation
Re
soient (x,y) , (x',y') 2 points de la courbe avec y = f(x)
(a,b) est centre de symétrie ssi x'+x = 2a et y'+y=2b c-à-d x' = 2a-x et y' = 2b-y
ou x'=2a-x et f(2a-x) = 2b - f(x)
ou x'=2a-x et f(2a-x) + f(x) = 2b
pour a = 0 x'= -x et f(-x) + f(x) = -2 et alors b = -1 et (,-1) est centre de symétrie
car f(-x) = (2x³-x²-10x+4)/(x²-4)
=> f(-x) + f(x) = -2.(x²-4)/(x²-) = -2
A+
Re-bonjour !
Merci de m'avoir répondu ! 
J'ai refait mes calculs pour la première et la deuxieme question et effectivement c= 1 et d=1
Pour la deuxième question j'ai fait le tableau de variations et j'ai trouvé que la fonction était
décroissante en - ; -2 / croissante en -2 ; 2 / décroissante en 2 ; +
; -2 / croissante en -2 ; 2 / décroissante en 2 ; + .
.
Par contre je n'ai pas compris ce que vous avez fait pour le centre de symétrie ! :S
Voila Merci
En faite en relisant, je viens de comprendre ce que vous avez fait donc je vais essayer de le refaire ! 
Merci
Re
Ta dérivée est
f'(x)= (2x4-14x²+40 )/ (x²-4)²
mais il manque un signe moins c'est
f'(x)= -(2x4-14x²+40 )/ (x²-4)²
comme (x²-4)² est tjs > 0 et que le delta de l'équation bicarrée (2x4-14x²+40 ) = 14²-8.40 = -124 est < 0 , cette fonction (2x4-14x²+40 ) est tjs positive
comme il y a 1 - devant , f '(x) est tjs < 0
et donc f décroît tjs
et ça colle avec le graphe que je t'ai posté
*
pour le centre de symétrie on commence par dire que ce centre est le milieu de 2 points de la courbe (x,y) et (x',y') => abscisse du centre = la demi somme des abscisses des 2 points de la courbe et idem pour les ordonnées
A+
Oui Je suis d'accord !
Mais pourquoi au début il y avait deux valeurs interdites 2 et -2 ?
Parce que je suis perdue je comprend plus ! 
Merci
Re
"" Mais pourquoi au début il y avait deux valeurs interdites 2 et -2 ? ""
car il y a (x²-4) au dénominateur et que -2 et 2 annulle x²-4 et qui donne donc 2 asymptotes verticales
A+
AHHHH Ok !! J'ai compris c'est bon ! 
Et comment on fait pour montrer que la droite (D) d'équation y= -2x-1 est une asymptote oblique de Cf ??
Merci
Re
AO c'est y = le ax+b du développement f(x) = ax + b + ( c / x-2 ) + ( d / x+2 )
car si y = mx+p est 1 asymptote oblique
on cherche le m = lim f(x)/x pour x -> + ou - l'infini
et le p en calculant lim de f(x) - mx pour x -> + ou - l'infini
A+
f(x)-(-2x-1)= (1/x-2) + (1/x+2)
lim [(1/x-2) + (1/x+2)] = lim [(1/x-2) + (1/x+2)] = 0
x -> +oo x -> -oo
ainsi
lim [f(x)-(-2x-1)] = lim [f(x)-(-2x-1)] = 0
x -> +oo x -> -oo
donc Cf admet une asymptote oblique d'équation y = -2x-1
Ok !! 
Merci beaucoup
Une dernière question 
Comment faire pour donner une équation de la tangente (T) à Cf au point I ??
Merci de m'aider c'est vraiment gentil
Re
l'équation de la tangente à la courbe au point (a,f(a)) est y = f '(a)(x-a) + f(a)
=>
en (0,-1) on a y = -5/2(x) + 1
A+