Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

limites fonctions exponentielles

Posté par
miraachalak 19-03-16 à 17:51

Saluttt !! j'ai a calculer les deux limites suivantes pourriez vous me dire si j'ai fait une erreur?

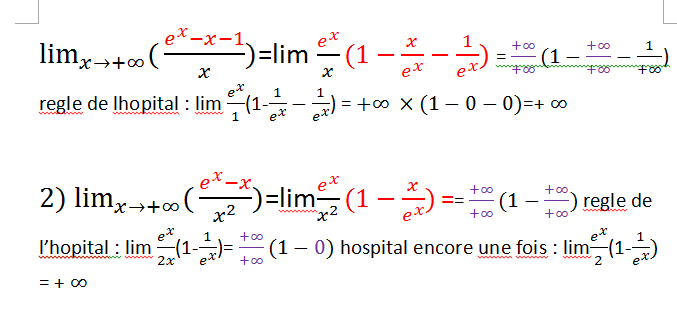
limites fonctions exponentielles

Posté par
Nicolas_75 Correcteurre : limites fonctions exponentielles 19-03-16 à 17:59

Bonjour,

Pas besoin d'invoquer L'Hopital. La limite de \dfrac{e^x}{x} est une question de cours.

Posté par
miraachalakre : limites fonctions exponentielles 20-03-16 à 19:15

Merciii pour votre reponse ouii je connais cela dans le cours mais j'ai voulu  cette methode peut-on la considerer correct?

Posté par
miraachalakre : limites fonctions exponentielles 20-03-16 à 19:16

J'ai voulu essayer*

Posté par
miraachalakre : limites fonctions exponentielles 21-03-16 à 19:13

Nicolas_75 @ 19-03-2016 à 17:59

Bonjour,

Pas besoin d'invoquer L'Hopital. La limite de \dfrac{e^x}{x} est une question de cours.
Merciii pour votre reponse  ouii je connais cela dans le cours mais j'ai voulu  essayer cette methode peut-on la considerer correct?

Posté par
miraachalakre : limites fonctions exponentielles 21-03-16 à 19:14

Nicolas_75

Posté par
Nicolas_75 Correcteurre : limites fonctions exponentielles 21-03-16 à 19:40

Peux-tu préciser quelle version précise de la règle de L'Hôpital tu appliques ?

Posté par
miraachalakre : limites fonctions exponentielles 21-03-16 à 19:56

Salut , lim u/v =lim u'/v' a l'infini

Posté par
miraachalakre : limites fonctions exponentielles 21-03-16 à 19:58

A chaque fois que j'ai eu infini/infini (marqué en mauve) j'ai trouvé la derivee du numerateur et celle du denominateur de LA FRACTION EN QUESTION

Posté par
Nicolas_75 Correcteurre : limites fonctions exponentielles 21-03-16 à 20:07

Pourquoi tu n'appliques pas directement à la règle à l'expression de départ ?

Posté par
miraachalakre : limites fonctions exponentielles 21-03-16 à 20:15

Parceque c'est infini -infini au numerateur qui ne donne pas nexessairement infini non?

Posté par
Nicolas_75 Correcteurre : limites fonctions exponentielles 21-03-16 à 20:24

Je vois.

Pour la première :

\dfrac{e^x-x-1}{x} = \dfrac{e^x}{x}-1-\dfrac{1}{x}

Le premier terme tend vers +oo (cours ou L'Hôpital), le deuxième est constant et le troisième tend vers 0. Donc le tout tend vers +oo

Pour la seconde :

\dfrac{e^x-x}{x^2} = \dfrac{e^x}{x^2}-\dfrac{1}{x}

Le premier terme tend vers +oo (L'Hôpital ou remarquer que \dfrac{e^x}{x^2}=\dfrac{1}{4}\,\left(\dfrac{e^{x/2}}{x/2}\right)^2) et le deuxième vers 0. Donc le tout tend vers +oo

Posté par
miraachalakre : limites fonctions exponentielles 22-03-16 à 14:39

MILLE MERCII Pour cette reponse trop claire Nicolas_75 !!!  juste une petite question si vous me permettez : si on a  n'importe  quelle expression et on obtient en calculant les limites \frac{\infty }{\infty } (6-\frac{4}{\infty }-\frac{0}{0} ) pourrai-je appliquer L'Hopital SEULEMENT a la fraction la ou j'ai 0/0 et a l'autre la ou j'ai infini/infini sans toucher au 6 et a 4/infini ?

Nicolas_75 @ 21-03-2016 à 20:24

Je vois.

Pour la première :

\dfrac{e^x-x-1}{x} = \dfrac{e^x}{x}-1-\dfrac{1}{x}

Le premier terme tend vers +oo (cours ou L'Hôpital), le deuxième est constant et le troisième tend vers 0. Donc le tout tend vers +oo

Pour la seconde :

\dfrac{e^x-x}{x^2} = \dfrac{e^x}{x^2}-\dfrac{1}{x}

Le premier terme tend vers +oo (L'Hôpital ou remarquer que \dfrac{e^x}{x^2}=\dfrac{1}{4}\,\left(\dfrac{e^{x/2}}{x/2}\right)^2) et le deuxième vers 0. Donc le tout tend vers +oo

Posté par
Nicolas_75 Correcteurre : limites fonctions exponentielles 22-03-16 à 14:45

Je n'aime pas cette façon de rédiger, mais partons de ton \dfrac{\infty }{\infty } \left(6-\dfrac{4}{\infty }-\dfrac{0}{0} \right)

Oui, tu peux appliquer L'Hôpital séparément à \dfrac{\infty }{\infty } et \dfrac{0}{0}.

Mais tu ne peux rien en déduire à ce stade. Il faut voir vers quoi tendent \dfrac{\infty }{\infty } et \left(6-\dfrac{4}{\infty }-\dfrac{0}{0} \right)

Si le premier facteur tend vers +\infty et le second vers 6, tu pourras en déduire que le tout tend vers +\infty

En revanche, si le premier facteur tend vers 0 et le second vers +\infty, tu ne peux pas conclure sur la limite de l'ensemble, du moins avec cette méthode.

Posté par
miraachalakre : limites fonctions exponentielles 22-03-16 à 14:49

Nicolas_75 MERCIIII BEAUCOUPP oui j'ai compris ton idee ma question etatit juste si on peut applique l'hopital separement sans besoin de modifier la forme de mon expression et vous m'avez repondu !! Merciii beaucoupp !!!

Posté par
Nicolas_75 Correcteurre : limites fonctions exponentielles 22-03-16 à 14:53

Je t'en prie.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1750 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !