salut

quel est l'énoncé exact ? ln(1+x)<ax ?

Bonjour,

Plus probablement

Un dessin:

Bonsoir cailloux,

Tu as très sûrement raison

merci d'avoir répondu, oui désolé j'ai pas vu, c'est bien  lnx<ax
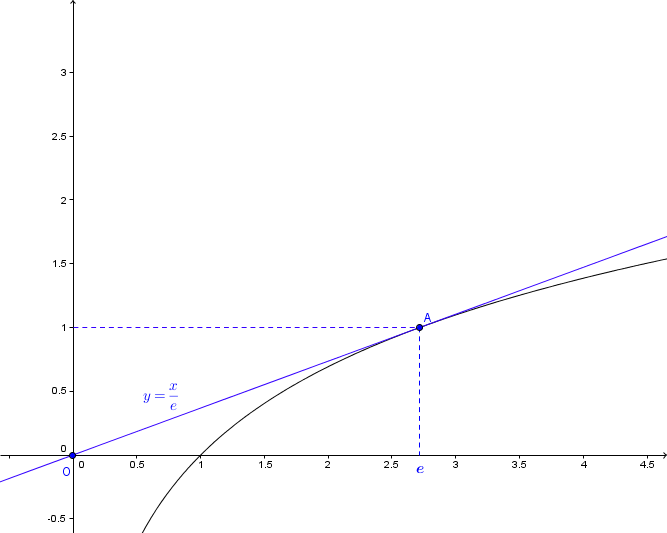
Je ne comprends pas très bien la courbe, je ne vois pas pourquoi y=x/e ?

Ton exercice revient à chercher pour quelle(s) valeur(s) de , on a, pour tout ,

D' où l' idée d' étudier la fonction définie sur par

On trouve (à toi d' étudier les variations de ), qu' elle admet un maximum en

Donc sur

sur

Autrement dit, si , on est certain que ou encore que

Le cas est illustré par la figure de 19h36.

oui d'accord je comprend mieux merci
j'ai trouvé que lnx/x était croissant sur ]0,e[ puis décroissant sur ]e,+infini[
et que comme la dérivée s'annule pour x=e f admet bien un maximum !
Après l'interprétation graphique grâce à votre courbe je comprends que si a>=1/e alors lnx<=ax mais je vois pas trop comment interpréter cette droite x/e ?
  

La droite d' équation est la tangente au point à la courbe représentative de la fonction logarithme.