Bonjour, j'ai un exercice de maths sur les les logarithmes.

Soit la fonction f définie sur telle que :
avec a, b, c des réels.

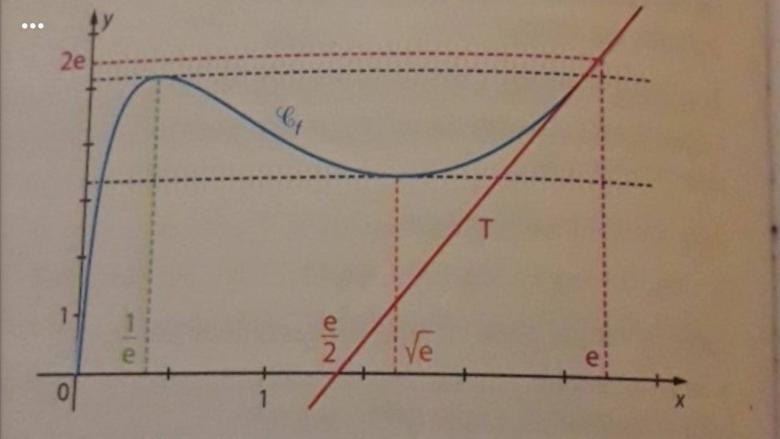
Sa courbe représentative C_f dans un repère orthogonal est donnée ci-dessous. T est la tangeante à au point d'abscisse e.
Les tangeantes )à au point d'abscisse et sont horizontales

1. a) Exprimer f'(x) en fonction de a, b et c.

b) A l'aide des informations précédentes et de celles notées sur le graphique, déterminer graphiquement les valeurs de, et .

c) En déduire que, pour tout x, de ]0;+\infini[ :
.

2. a) Montrer que pour tout x on a :


b) En déduire le tableau de variation de f où on précisera les valeurs exactes des extrema locaux.

J'ai essayé ça pour la 1. a) mais j'ai peur de me tromper ?




Merci de votre aide