Inscription / Connexion Nouveau Sujet
Maths DM
Bonjour, je n'arrive pas à faire cet exercice qui est dans mon DM de maths
Voici l'énoncé:
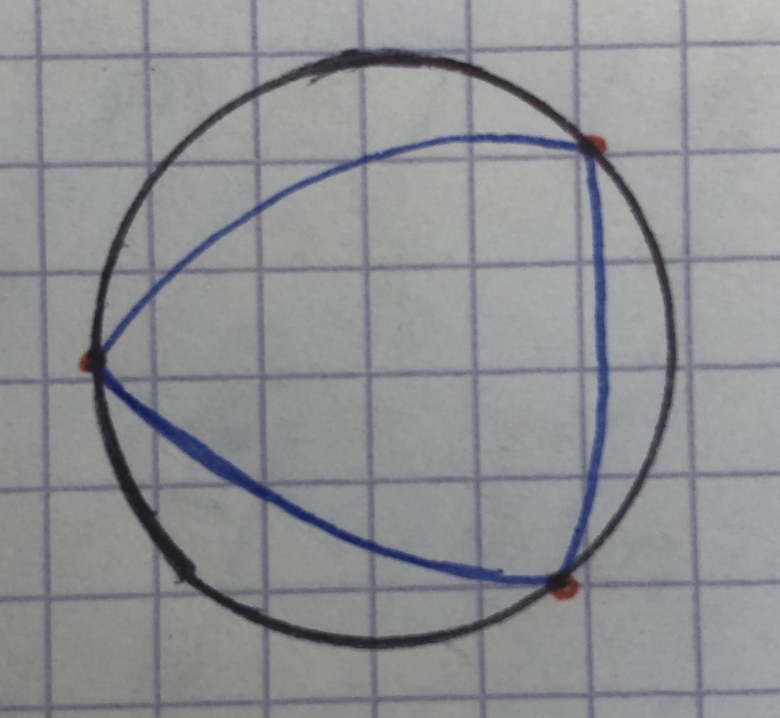
Chaque point rouge de ce cercle est le centre d'un cercle passant par les deux autres. Démontrer que la longueur du cercle noir est 2/racine de 3 fois plus grande que celle du tracé bleu.
Merci d'avance pour votre aide.
Bonjour Leile, pour l'instant, je n'ai pas fait grand chose car je n'arrive pas à me lancer.
cependant je me disais qu'il fallait peut être que je commence par calculer le périmètre du cercle noir et ensuite du tracé bleu mais je ne sais pas comment faire . Peut tu m'aider stp?
pour calculer les perimètres, il te faut les rayons...
Essayons de définir les rayons.
complète ta figure :
nomme les 3 points rouges A, B, C.
montre que le triangle ABC est équilatéral ==> déduis en la mesure des angles.
place le centre du cercle noir : O
et trace la hauteur BH (qui passe par O, puisque ABC est équilatéral).
dis moi si c'est clair, et on continue.
pour calculer les perimètres, il te faut les rayons...
Essayons de définir les rayons.
complète ta figure :
nomme les 3 points rouges A, B, C.
montre que le triangle ABC est équilatéral ==> déduis en la mesure des angles.
place le centre du cercle noir : O
et trace la hauteur BH (qui passe par O, puisque ABC est équilatéral).
dis moi si c'est clair, et on continue.
Merci, mais est ce que je peux dire que le triangle est equilateral même si les tracé bleu sont arrondie ? Cependant si oui, les angles feront 60 degrés
tu ne lis pas bien mes posts, je crois..
en bleu, ce sont des arcs de cercles, ces tracés sont arrondis, bien sûr.
Moi, je te dis de tracer le triangle ABC ==> un triangle a 3 cotés, qui ne sont pas arrondis.. ..
pour qu'on parle de la même chose, fais la figure comme ceci :
Effectivement j'avais mal compris ce que tu m'as dit, grâce à ta figure je comprend mieux ce que tu as voulu m'expliquer.
il est inutile de rappeler mes messages à chaque fois, ça prend de la place et ça ne sert à rien : on est juste tous les deux..
pourquoi ABC est il équilatéral ? tu dois le justifier.
ensuite si ABC est équilatéral, l'angle ABC mesure 60°.
que mesure l'angle AOC ?
déduis en l'angle HCO.
est ce que sa marche si je dis que le triangle ABC est équilatéral car toutes les droites remarquables sont confondus.
le triangles AOC est isocèle et HOC est triangle recangle ? je ne sais pas coment mesurer les angles.
"est ce que sa marche si je dis que le triangle ABC est équilatéral car toutes les droites remarquables sont confondus."
non, c'est parce qu'il est équilatéral que les droites sont confondues, et pas l'inverse... Rien ne dit dans l'énoncé que les droites sont confondues.
d'après l'énoncé :
A et C sont sur le cercle de centre B ==> BA = BC,
B et C sont sur le cercle de centre A ==> AB = AC
donc AB = AC = BC ==> ABC est équilatéral.
AOC est isocèle : oui, car OA et OC sont des rayons du cercle noir.
ABC = 60°, c'est un angle inscrit qui intercepte l'arc AC.
AOC est l'angle au centre qui intercepte le même arc ==> AOC = 120° (cours de 3ème).
puisque AOC est isocèle, et que l'angle AOC mesure 120°, HCO mesure 30°
(tu aurais pu aussi remarquer que CO est bissectrice de ACB)..
on a bien avancé sur la mesure des angles.
exprime le cos de HCO en te placant dans le triangle HCO rectangle en H.
(rappel cos = adjacent / hypoténuse).
cos HCO = HC / CO oui,
après, je ne vois pas où tu as trouvé 30/90 : ça, ça ne veut rien dire..
HCO mesure 30° donc cos HCO =  3/2
3/2
ainsi  3/2 = HC/CO
3/2 = HC/CO
et CO = ????
CO : rayon du cercle noir. ==> périmétre du cercle noir = ??
HC : la moitié du rayon CA ==> CA = 2 HC
comment exprimes tu la longueur des 3 arcs de cercles bleus ?
Guigui07,
tu écris n'importe quoi ! est ce que tu es sérieux ?
tu es en 1ère S ? il faut vraiment que tu te reprennes, si tu veux réussir dans cette voie..
tu mélanges les distances, les angles, les cos...
HC = 90° ????? un segment = 90° ?? 
à partir de
tu en déduis que CO = ????
non, il suffit de faire un produit en croix (comme au collège) pour écrire que
et 2HC = CA donc
CO : rayon du cercle noir. ==> périmétre du cercle noir = 2 * pi * CO
comment exprimes tu la longueur d'un arc de cercle d'un angle de 60° ?
et de 3 arcs de cercles de 60° ? (les bleus)
Excuse moi de ne pas comprendre mon exercices, cependant je n'avais pas compris toute tes explications.
je ne comprend pas comment comment on mesure CA .
je ne te reproche pas de ne pas comprendre l'exercice, ça, ça peut arriver à tout le monde, et nous sommes là tous les deux pour ça.
je te reproche d'écrire des choses qui n'ont pas de sens : ça, tu peux l'éviter. Tu dois et concentrer, et faire attention à ce que tu écris.
tu n'as pas à mesurer CA : on ne peut pas le mesurer. On garde CA. C'est le rayon des cercles bleus.
tu sais que le perimetre d'un cercle de rayon CA = 2 * pi * CA.
comment exprimes tu la longueur d'un arc de cercle d'un angle de 60° et de rayon CA ?
D'accord merci, pour exprimer la longueur d'un arc de cercle d'un angle de 60° et de rayons CA je fait :
(60x xCA)/180
xCA)/180
oui, c'est correct.
ou plus exactement 2*pi*CA * 60/360 = 2 * pi * CA * 1/6
ca, ca te donne la longueur d'un arc bleu,
or on en a 3
donc longueur "bleue" = 3* 2 * pi CA * 1/6 = pi * CA
on est presque au bout.
on a vu que longueur noire = 2 * pi * CO
avec
reprends la question de l'énoncé.. est ce que tu sais conclure ?
je n'ai pas bien compris pourquoi tu as fait cela: "2*pi*CA * 60/360 = 2 * pi * CA * 1/6"
et pour la conclusion est ce que CA=2 d'après l'énoncé?
Peut tu encores m'aider pour la conclu stp ?
Merci
"2*pi*CA * 60/360 = 2 * pi * CA * 1/6"
par ce que 60/360 = 1/6 ..
CA= 2 : non, on ne te demande pas CA, et tu ne peux pas calculer CA (on l'a vu déjà).
la question est :
tu dois montrer que longueur noire = longueur bleu * 2/ 3
3
on a trouvé
longueur noire = 2 * pi * CO avec
d'ou longueur noire =
on a trouvé longueur "bleue" = pi * CA
donc longueur bleue * 2/ 3 = pi * CA * 2/
3 = pi * CA * 2/ 3 = longueur noire
3 = longueur noire
CQFD.
Je te résume la démarche (j'ai l'impression que c'est nécessaire !).
On a voulu exprimer les longueurs noires et bleues en fonction du rayon du cercle bleu.
ce sont des perimètres de cercles ==> il nous faut les rayons.
pour exprimer le rayon CO, on s'est placé dans le triangle OHC rectangle en H (pour y arriver, on est partis du triangle ABC équilatéral), et avec cos, on a exprimé CO en fonction de CA : on a donc exprimé le rayon noir en fonction du rayon bleu.
avec les rayons, on a exprimé les longueurs noire et bleue en fonction de CA,
pour conclure.
Je te recommande :
- d'assimiler la démarche.
- de reprendre cet exercice seul, pour savoir le refaire.
- de ne pas oublier la question de départ, quand tu fais un exercice..
- de revoir tes cours de collège (théorèmes, propriétés, calcul littéral, simplification de fractions, etc..).
- de bien faire attention à ce que tu écris (ne mélange pas les segments, les angles, etc..), et aux unités.
Bon courage.


