il s'agit de tracer une approximation de la courbe en calculant des valeurs "discrètes" (à la différence de graphes réels qui représentent les valeurs continues) petit à petit;

quelle valeur t'impose-t-on pour q(0) ?

S'il s'agit d'intégrer cette équation différentielle, tu peux remarquer qu'elle est à variables séparables.

@Priam : oui, elle est intégrable, mais l'énoncé cherche avant tout à présenter une méthode d'approximation, sinon à quoi riment le titre et la donnée d'un 'pas' ?

q(0)=0 apres jessaie de trouver q'(0) jobtiens 1/20 apres comme je fais avec le pas parce ke je suis censée obtenir une courbe croissante mais mes valeurs sont bizarres jobtiens des valeurs positives puis des valeurs negatives. EN fait je ne sais pas integrer le pas dans les deux équations que j'ai trouvée.

L'idée de la méthode d'Euler c'est de mettre l'équation sous la forme q'(t)=(5-q(t))/100 et se demander ce qui se passe si on ne place à un temps t assez petit. On dit alors en assimilant la dérivée q'(t) à son accroissement que q= [(5-q(0))/100]t
cela fournit une approximation de q : q₁(t)= q(0)+q à l'instant t₁=t et puis on recommence. Est-ce bien ça que tu as fait ?

j'ajoute mon grain de sel :

rappel : le nombre dérivé est la limite du taux de variation

dans une simulation, on estime que si l'écart est suffisamment petit, on a une bonne approximation de ce nombre dérivé
dans ton exercice bourrin, h=30, donc la notion de suffisamment petit est très fonction du contexte.

que dit ton équation ?


la limite du taux de variation en chaque point est fonction de la valeur de la fonction en ce point

remplaçons q' par le taux



ce qui permet d'établir que dans cette approximation, on peut calculer de proche en proche une valeur approximative de q(x+h) si on a une valeur de q(x)



donc avec q(0)=0, on calcule q(0+h)=q(h)
puis avec q(h), on calcule q(h+h)=q(2h)
puis avec q(2h), on calcule q(2h+h)=q(3h)
etc...

il se trouve que ton équation possède aussi une solution exacte :

Ainsi, on peut comparer la solution approximative obtenu avec la solution exacte

voici le résultat sous tableur :


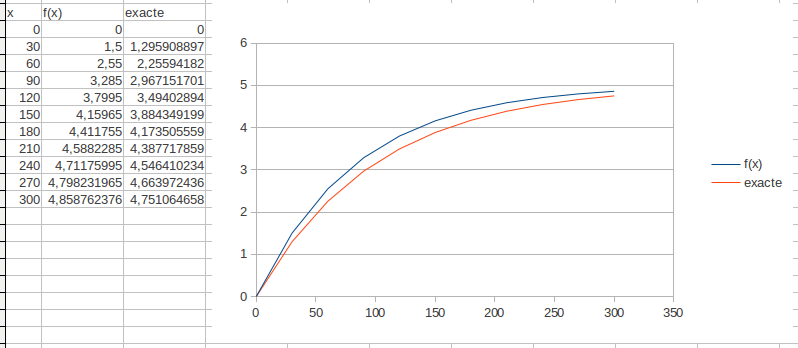
évidemment, si le pas est plus fin, le nombre de calculs à faire est plus important, mais le résultat approximatif est plus proche du résultat théorique.

Cette méthode est très utile pour se faire une idée du graphe obtenu
elle n'est possible que si on a une valeur particulière à notre disposition et si on peut mettre l'équation initiale sous la forme q(x+h) = FONCTION(q(x))

correction typographique :
taux de variation :

Evidemment là avec un pas de 30s qui est plutôt grand, on s'éloigne pas mal de la solution après 300s


(Essaye geogebra pour dessiner, on trouve des feuilles toute faites sur Euler)

oui tu as raison dhalte, il ne va pas mon dessin, j'ai dû me tromper quelque part.