Inscription / Connexion Nouveau Sujet
maths fonction dérivée
bonjour j'ai un exercice en maths sur les fonctions dérivées a faire avant le 20 avril et j'aurai besoin d'aide s'il vous plait
Une société fabrique des pièces pour l'aéronautique.
Le bénéfice de l'entreprise, en euros, B est donné en fonction du rang n du mois par
:B(n) = n3-21n2+ 120n+ 4500
problématique: quel est le bénéfice maximal possible?
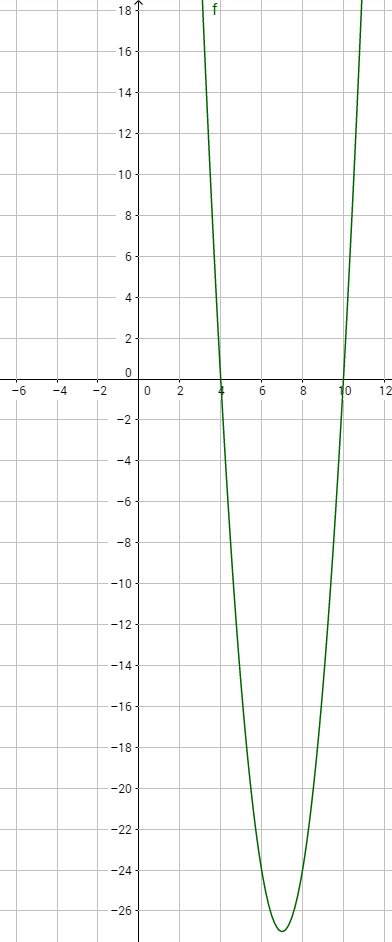
Soit la fonction f définie pour tout nombre réel x de l'intervalle [1; 12] par:
f(x) = x3-21x2+120x+4500
question 1: déterminer f'(x).f' étant la fonction dérivée de la fonction f.
question 2: calculer f'(1) et f' (12) puis indiquer le signe de ses deux dérivées.
question 3:résoudre l'équation f'(x)=0
merci de me répondre au plus vite
Bonsoir,
Il faudrait essayer de chercher avant de demander la correction 
Soit la fonction f définie sur [1 ; 12] par :
1)
2)
3)
3x² - 42x + 120 = 0
 = b² - 4ac
= b² - 4ac
=(-42)² - 4 3
3 120
120
= 324 > 0 l'équation admet 2 solutions notées et
.
=4
= 10
Il faudrait essayer de chercher avant de demander la correction

il faudrait aussi, peut-être, donner des indications pour aider la personne et non pas lui faire l'exercice... en contrôle, la personne n'aura pas cette aide et ne saura peut-être pas refaire.
petite remarque sur la rigueur Krayz, dans ton tableau de variations, il s'agit des variations de la fonction f et non pas de f(x)
Oui je sais cette remarque ma déjà été faite sur le forum mais mon professeur accepté et écrit même comme ça pour les corrections.
malou dit la même chose 
signe de f'(x)
variations de f (car ce sont les variations de la fonction, et la fonction c'est f et non f(x) )

D'accord 
En "français", je sais bien que cela veut dire « variations de la fonction » de toute façon 
De nombreuses personnes sur les forums/sites de maths/cours vidéo utilisent f'(x) ainsi que mon professeur... 
That's so strange 
f'(x) je suis d'accord pour le signe de la dérivée
mais les variations, c'est f
(mais c'est une imprécision qu'on rencontre souvent)
De nombreuses personnes sur les forums/sites de maths/cours vidéo utilisent f'(x) ainsi que mon professeur...

f(x) *
Oui en effet ^^
je sais....c'est fort dommage, car qd on l'apprend aux élèves dès le départ, cela devient totalement naturel ensuite
il s'agit pas de pénaliser pour ça, mais de reprendre systématiquement les erreurs et plus on avance, mieux on rédige
Oui^^
Mais malgré le fait que ma prof accepte cette écriture (fausse) je vais quand même écrire "variations de f" lors du prochain DS (dans 2 semaines).
f'(x) est donc juste ?



