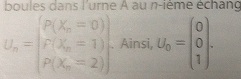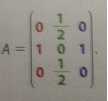Inscription / Connexion Nouveau Sujet
Matrice
Bonsoir,
On modélise la situation par des urnes contenant des boules identiques.
On suppose qu'on a placé initialement deux boules dans l'urne A.
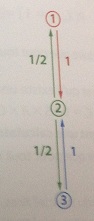
Les urnes peuvent ensuite se trouver dans trois situations possibles:
(1) les deux boules sont dans l'urne A
(2) chaque urne contient une boule
(3) les deux boules sont dans l'urne B
Pour tout entier naturel n, on note Xn la variable aléatoire donnant le nombre de boules dans l'urne A au n-ième échange, et la matrice des probabilités:
Un=(voir photo) Ainsi, Uo
1) Montrer que pour tout entier n 0, Un+1=AUn, où A=(voir photo)
0, Un+1=AUn, où A=(voir photo)
2) En déduire que pour tout entier n 0 Un=A^n*Uo
0 Un=A^n*Uo
3)Conjecturer la valeur de A^n en fonction de n, puis démontrer la conjecture
4) La répartition des boules se stabilise-t-elle lorsque le nombre d'échanges devient grand?
Je n'arrive pas à montrer ma conjecture qui est que A^n converge vers la matrice
(0,5 0 0,5
0 1 0
0,5 0 0,5) pour n pair
et n impair on a
(0 0,5 0
1 0 1
0 0,5 0)
Bonsoir :
On modélise la situation par des urnes contenant des boules identiques.
Quelle situation ?
Pour t'aider, il faudrait que tout le problème soit là !
Mathx96
Désolé j'ai oublié
On considère deux urnes, A et B et N particules réparties dans les deux urnes.
A chaque étape, on choisit au hasard une particule et on la change d'urne
Dans notre exemple N=2
soit le nombre de boules dans l'urne A
u_1=0
1
0
c'est le vecteur des probabilites des vaelurs de
et ce sera la forme de tous les u_n avec n impair donc l'esperance de quand n impair c'est 0*0+1*1+2*0=1 et
si n pair u_n=0.5
0
0.5
si n pair esperance de X_n = 0.5*0+0*1+0.5*2=1 donc vaut toujours 1 donc si on regarde lea moyenne des resultats sur un grand nombre d'echanges, il ya aura un boule dans A et .. une boule dans B
cet exercice concerne les urnes d'Ehrenfest: il ya beaucoup de textes la dessus sur internet ici N=2
Alors pour la 3 : Ta conjecture est bonne mais exprime la en fonction des puissances de A.
Pour la démo, utilise on pourra utiliser un récurrence forte.
Pour la 4 :
Si le système admet un état stable, alors il existe un vecteur colonne S tel que :
Si on écrit
Cela revient à dire que
Ou alors en effectuant le produit matriciel :
On peut alors associer à cette égalité un système :
Tu peux alors essayer de le résoudre :
S'il y a un seul triplet solution , alors le vecteur
est appelé état stable du système et la suite converge vers lui.
S'il y a une infinité de solutions, ou s'il n'y en a pas, alors le système n'admet pas d'état stable ; la suite n'a pas de limite et le système continuera de changer d'état constamment.
Bon courage !
Mathx96