Inscription / Connexion Nouveau Sujet
Minimum ; Maximum d'une fonction 
Bonsoir tout le monde, la famille va bien, les voisins, les habitants de la ville, de la france? 
J'ai un DS demain sur les fonctions et je n'ai pas compris quelque chose dans un exercice qu'elle nous a donné pour s'entraîner :s .
Sujet :
Soit f une fonction sur I, dont on donne le tableau de variation. Déterminer pour chaque cas, s'ils existent, le minimum et le maximum de f sur I
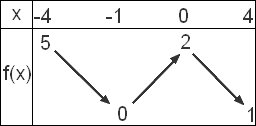
a) I =[-4;4]
(voir 1er document attaché)
b) I=[-5;+oo]
(voir 2eme document attaché)
Donc le maximum de la première fonction est 5 atteint en x=-4
Le minimum de la 1ere fonction est 0 atteint en x=-1
Le maximum de la 2eme fonction est 2 atteint en x=-2 et x= 3
Le minimum ... ?
Je bloque :s .
Dans l'énnoncé on nous dit "s'ils exisent le minimum et le maximum.
Pour la 2eme fonction il y aurait t'il aucun minimum?
Merci d'avance pour toutes vos réponses 
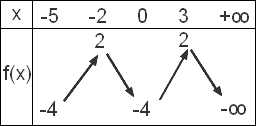
Pour la 2eme fonction il n'y a pas de minimum à cause la limite en +inf qui vaut -inf, la fonction "descend" vars -inf donc pas de minimum


