Inscription / Connexion Nouveau Sujet
Mise en équation
Bonjour,
Je n'arrive pas à résoudre cet exercice :
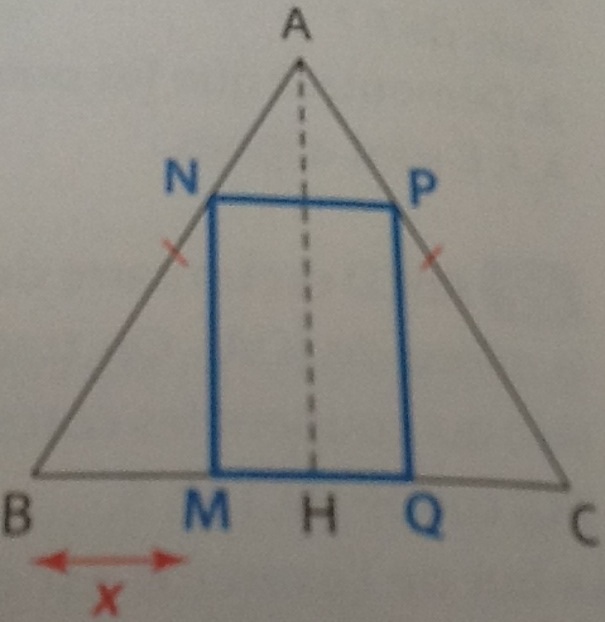
ABC est un triangle équilatéral de côté 6. M est un point de [BH]. MNPQ est un rectangle d'axe de symétrie (AH).
Le but de l'exercice est de placer M sur [BH] tel que MNPQ soit un carré. On pose BM = x.
1.a) Calculez MN en fonction de x.
b) Justifiez que MQ = 6-2x.
2.a) Justifiez que le problème posé revient à résoudre l'équation x(racine carrée de 3) = 6-2x.
b) Déduisez-en x et démontrer que la valeur trouvée s'écrit également 6(2-racine carrée de 3).
Pour la 1.a), j'ai commencé à faire :
Soit les triangles BNM et BAH tels que (MN) parallèle à (HA).
BN/BA = BM/BH = MN/HA soit BN/6 = x/3 = MN/HA, mais cela ne me permet pas de trouver MN...
Pouvez-vous m'aider svp ?
Donc avec le théorème de Pythagore, j'ai trouvé AH = 3racine carrée de 3.
Et donc, avec le théorème de Pythagore, BN/6 = x/3 = MN/3racine carrée de 3, soit MN = x(3racine carrée de 3)/3.
C'est bien ça ? 
Super !
Pour la 1.b), j'ai démontré que CQ = x. D'où BM = QC = x. Par conséquent, BC = BM + MQ + QC = 6. Donc x+MQ+x = 6 ; MQ = 6 -2x.
J'ai réussi à faire la 2.a) mais je n'arrive pas du tout à faire la 2.b)...
Pouvez vous m'aider une dernière fois s'il vous plaît ?
Tu dois résoudre x racine de 3= 6 - 2x.
Tu vas trouver x= 6 sur (2 + racine 3).
Pour montrer que cette valeur est aussi égale à 6(2 - racine3), tu multiplieras la valeur de x par la fraction (2- racine3) sur (2 - racine3), ce qui ne change rien puisque cette fraction est égale à 1.
Ainsi, au numérateur tu auras un produit remarquable de la forme ( a + b)(a - b), qui va se simplifier.
Tu auras alors ce qu'on te demande.


