Inscription / Connexion Nouveau Sujet
Modéliser
Bonjour, Pouvez-vous m'aider et me dire si mes réponses sont correctes ?
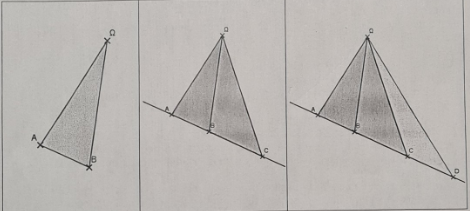
On relie un point Ω à d'autres points d'une droite du plan et on s'intéresse aux triangles obtenus. On cherche à savoir combien on obtient de triangles en reliant un point Ω à un point, à deux points puis à trois points etc. (Voir pièce jointe)
1. a) Quel est le nombre de triangles obtenus si on relie Ω à un point ?
0 triangle
b) Quel est le nombre de triangles obtenus si on relie Ω à deux point ?
1 triangle (ABΩ)
c) Quel est le nombre de triangles obtenus si on relie Ω à trois point ?
3 triangles (ABΩ ; BCΩ ; ACΩ)
d) Quel est le nombre de triangles obtenus si on relie Ω à quatre point ?
6 triangles (ABΩ ; BCΩ ; CDΩ ; ACΩ ; BDΩ ; ADΩ)
2. Forme Récurrente :
n est un entier supérieur ou égal à 2. On note tn le nombre de triangles obtenus en reliant Ω à n points d'une droite du plan.
a) Combien de triangles supplémentaires obtient-on si on ajoute un (n+1)-ième point ?
b) Exprimer tn+1 en fonction de tn
c) Etudier le sens de variations de la suite (tn).
d) Compléter l'algorithme ci-dessous qui permet de déterminer le terme de rang n.
Fonction terme(n)
t<---.......
pour i allant de 1 à n-2
t <----...........
Fin pour
Retourner.........
e) Déterminer le nombre de triangles qu'on obtient en reliant Ω à 26 points distincts d'une droite du plan. Expliquer la démarche.
3. Conjecture de la forme explicite.
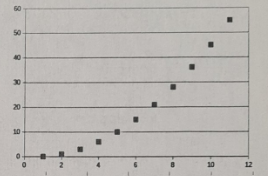
A l'aide d'un tableur on a obtenu le nuage de points qui représente la suite (tn).
Les points semblent être sur une parabole, déterminer l'équation de cette parabole et conjecturer la forme explicite de (tn).
Je vois que pour passer de 3 triangles à 6 triangles, on augment de 3=n
Mais je ne comprend pas comment le noter.
Bonjour, Pouvez-vous m'aider et me dire si mes réponses sont correctes ?
On relie un point Ω à d'autres points d'une droite du plan et on s'intéresse aux triangles obtenus. On cherche à savoir combien on obtient de triangles en reliant un point Ω à un point, à deux points puis à trois points etc. (Voir pièce jointe)
1. a) Quel est le nombre de triangles obtenus si on relie Ω à un point ?
0 triangle
b) Quel est le nombre de triangles obtenus si on relie Ω à deux point ?
1 triangle (ABΩ)
c) Quel est le nombre de triangles obtenus si on relie Ω à trois point ?
3 triangles (ABΩ ; BCΩ ; ACΩ)
d) Quel est le nombre de triangles obtenus si on relie Ω à quatre point ?
6 triangles (ABΩ ; BCΩ ; CDΩ ; ACΩ ; BDΩ ; ADΩ)
2. Forme Récurrente :
n est un entier supérieur ou égal à 2. On note tn le nombre de triangles obtenus en reliant Ω à n points d'une droite du plan.
a) Combien de triangles supplémentaires obtient-on si on ajoute un (n+1)-ième point ?
Si on ajoute un (n+1)-ième point on obtient tn+n triangles supplémentaires.
b) Exprimer tn+1 en fonction de tn
tn+1=tn+n
c) Etudier le sens de variations de la suite (tn).
t1=0
t1+1=t1+1
t2=0+1
t2=1
Donc t2>t1 ainsi tn+1>tn donc la suite est strictement croissante pour tout n ∈ ℕ
d) Compléter l'algorithme ci-dessous qui permet de déterminer le terme de rang n.
Fonction terme(n)
t<---.......0
pour i allant de 1 à n-1
t <----...........t+i
Fin pour
Retourner.........t
e) Déterminer le nombre de triangles qu'on obtient en reliant Ω à 26 points distincts d'une droite du plan. Expliquer la démarche.
En utilisant le programme précédant, le nombre de triangles qu'on obtient en reliant Ω à 26 points distincts d'une droite du plan est de 325.
3. Conjecture de la forme explicite.
A l'aide d'un tableur on a obtenu le nuage de points qui représente la suite (tn).
Les points semblent être sur une parabole, déterminer l'équation de cette parabole et conjecturer la forme explicite de (tn).
a+b+c=0 c=-a-b c=-a-b
4a+2b+c=1 => 4a+2b-a-b=1 => 3a+b=1
9a+3b+c=3 9a+3b-a-b=3 8a+2b=3
c=-a-b c=-a-b c=-a-b c=-a-b
b=1-3a => b=1-3a => b=1-3a => b=1-3a
8a+2(1-3a)=3 8a+2-6a=3 2a=1 a=1/2
c=-1/2-b c=-1/2-b c=-1/2+1/2=0
b=1-3(1/2) => b= -1/2 => b=-1/2
a=1/2 a=1/2 a=1/2
Donc tn = an²+bn+c
tn = (1/2)n² + (1/2)n