bonsoir

il faut montrer que pour tous réels, il est possible d'avoir une image de ce réel par f

donne ta fonction
.

La fonction est :

          x²-x+3
f(x) = -------------
         2x²+x+1

Les 2 trinômes n'ont pas de solution (∆<0), ça a un rapport ?

pour que ta fonction soit définie, puisque c'est une fraction, il faut que le dénominateur soit non nul

autrement dit, toutes les valeurs de x sauf celles annulant le dénominateur, auront une image

2x²+x+1 = 2(x²+x/2)+1 = 2( (x+1/4)²-1/16 ) +1 = 2(x+1/4)²+7/8
ce dénominateur est supérieur ou égal à 7/8 => il ne s'annule jamais

la fonction est définie pour tout x réel => Df = R

A vérifier
.

Merci pour ta réponse !

J'avais cherché la valeur interdite, mais il me restait un x...

Dans la suite de l'exerice, il y a une question :

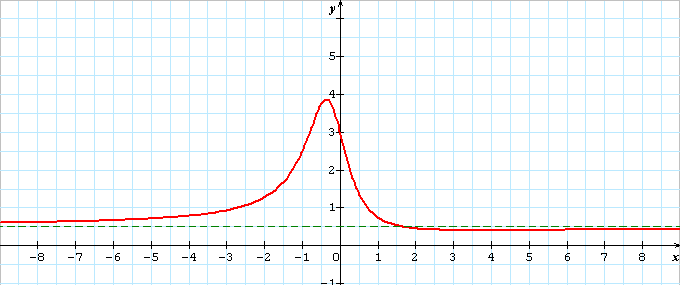
En utilisant le courbe f obtenue à l'aide d'une calculatrice, proposer 2 nombres m et M tels que m <ou= f(x) <ou= M.
Démontrer que cette conjoncture est exacte ?

Comment procéder ?

Merci.

En utilisant le courbe f obtenue à l'aide d'une calculatrice, proposer 2 nombres m et M tels que m <ou= f(x) <ou= M.
Heureusement que Casio et Texas Instrument sont là, sinon il faudrait quasiment demander aux élèves de TS de réfléchir.

salut otto, tu as oublié sine qua none

pour Nowak, la courbe pour tenter de déterminer m et M

A toi
.

Je ne connais pas sine qua none, est ce une marque de calculatrice?

non, un logiciel freeware dont borneo fait la promo
.

Bonjour, j'ai besoin d'aide :


f(x)= sin x / (2+cos x)

Justifier que f est définie sur

Merci

Bonjour
Alors ce serait par rapport à l'équation...
Je n'ai pas compris comment vous êtes passé de 2(((x+1/4)^2)-1/16)+1 à 2((x+1/4)^2)+7/8

Pourriez-vous m'expliquer? Merci d'avance

Parce que ma fonction à moi est x/x^2+x+1 et je ne sais pas comment faire

Bonjour

Une fraction existe si son dénominateur n'est pas nul.

Que faut-il vérifier ?

bonjour
@ waaradi
[quote]Parce que ma fonction à moi est x/x^2+x+1 et je ne sais pas comment faire[/quote


pour montrer que f est définie sur R, tu dois démontrer qu'il n'y a pas de valeur interdite.
C'est à dire que x²+x+1 n'est jamais nul.

bonjour Galouu17
Crée ton topic

Pour écrire une fraction sans utiliser LaTeX on écrit

(numérateur)/(dénominateur)

Sinon en respectant les règles de priorité entre opérations on n'arrive pas à ce que tu voudrais.

waaradi, lis ceci :

extrait de la FAQ du forum :

Q27 - Comment bien écrire une formule ?

Si vous ne savez pas ou ne souhaitez pas utiliser le LaTeX, il faut faire attention aux parenthèses lorsqu'on traduit une telle expression "en ligne" !

Exemple : prenons l'expression
Que faut-il écrire "en ligne" ?
A=2x-1/x-3 ? Non, ceci est égal à
A=2x-1/(x-3) ? Non, ceci est égal à
A=(2x-1)/x-3 ? Non, ceci est égal à
Il faut donc écrire : A=(2x-1)/(x-3)

D'ailleurs, c'est pareil sur une calculatrice ... Il ne faut pas oublier ces parenthèses, ou le calcul sera tout simplement faux.

Pensez, lorsque vous postez un énoncé sur le forum, à rajouter les parenthèses nécessaires pour que les autres membres puissent vous venir en aide sans avoir un doute sur l'expression donnée et sans devoir deviner ce que vous avez voulu écrire... Ainsi, chacun gagnera du temps.