Inscription / Connexion Nouveau Sujet
niveau seconde, exercice géométrie
Bonjour,
Pouvez vous s'il vous plait, me donner des indications ou résoudre la question suivante, merci:
énoncé:
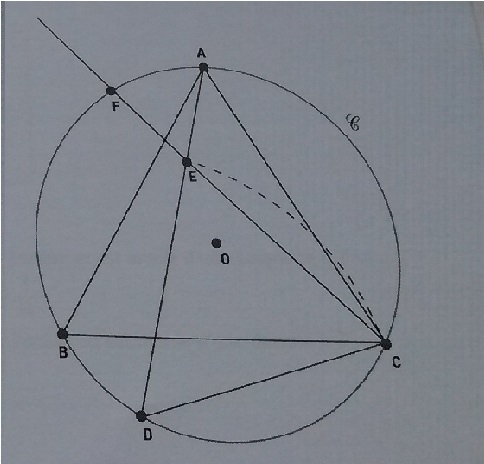
On considère un triangle équilatéral ABC, C son cercle circonscrit et O son centre . Soit D un point quelconque du petit arc [BC].
On note E le point du segment [AD] tel que DE=DC.
La droite [EC] recoupe le cercle C en un point appelé F.
Question:
Montrer que le triangle DEC est équilatéral
Merci beaucoup.
Cordialement
choco429
Bonjour
vous avez DE=DC donc le triangle DEC est isocèle
le triangle ABC est équilatéral par conséquent
deux angles interceptant le même arc sont de même mesure donc
les angles à la base sont de même mesure
je vous laisse conclure
Bonjour hekla,
Merci de votre réponse.
Quand vous dites:
deux angles interceptant le même arc sont de même mesure donc mes \widehat{EDC}=\dfrac{\pi}{3}
Est ce que c'est une propriété ? Pensez vous vraiment qu'elle est vrai ?
Il y a t-il une autre façon de résoudre cette question ?
Merci beaucoup.
Bonsoir
piste:
Par les angles : si les 3 angles sont égaux, alors le triangle est équilatéral
"On note E le point du segment [AD] tel que DE=DC. " => les angles DEC et ECD sont égaux
c'est une suggestion...
et oui, bonjour hekla
bien vu.
pour choco,
si la somme des 3 angles valent chacun 60°, alors le triangle est équilatéral
"On note E le point du segment [AD] tel que DE=DC. " => les angles DEC et ECD sont égaux
Et l'angle EDC ou ADC (puisque E appartient ) au côté AD , intercepte l'arc AC égal à 60°
Donc l'angle EDC=60° et forcément les 2autres valent chacun 60°
Non ce n'est pas une reprise d'étude.
En effet je suis en licence.
Cette exercice est celui de ma petit soeur, et j'avoue que la réponse doit être simple et évidente, mais j'ai un peu de mal.
Cordialement
choco429


