Inscription / Connexion Nouveau Sujet
Nombre de solution fonction
Bonjour
J'ai un petit soucis concernant cette exercice (en fichier joint).
A la question D, j'ai mis que l'affirmation est vrai car on a f(0)=4 et il y a une deuxième solution entre [2;+oo]. Pourtant j'ai eu faux.
Ai-je raté quelque chose ?
Merci d'avance.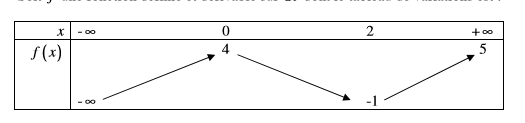
malou > image recadrée, fais l'effort de recopier ton énoncé si tu veux de l'aide oberyn
D) Equation f(x) = 4.
Pour x = 0, il y a une solution, car f(0) = 4 (c'est une solution double).
Il y a une autre solution dans l'intervalle [2; + oo).
Donc 2 solutions.
Oui c'est pourtant ce que j'ai marqué, que l'affirmation D est vraie mais pourtant dans le corrigé c'est marqué FAUX...
Erreur du corrigé ?
Et donc ?
Tout point de cette courbe admet une tangente, horizontale ou non...
On peut juste dire que f'(0) = 0, mais quel rapport avec une éventuelle "multiplicité" de 0 pour l'équation f(x) = 4 ?
La seule référence à ce terme de "solution double" que je connaisse, c'est par exemple dire que 4 est "solution double" de l'équation (x-4)² = 0 , mais pour autant ça ne veut pas dire que cette équation "admet deux solutions"...
Et en tous cas ça n'a rien à voir avec le fait que la courbe d'une fonction admet une tangente horizontale.
Si tu as une (ou des) référence(s) à ce sujet, je suis preneur 
Justement, il me semble, d'après le tableau de variation, que la fonction f(x) - 4 doit être de la forme ax²(x - b) , où b est la racine supérieure à 2 .
Le détail, c'est qu'il n'y a absolument aucune raison qu'il s'agisse d'une fonction polynôme , on peut avoir le même genre de situation avec une fonction exp par exemple, ou tout bêtement avec une fonction définie par une courbe (donc sans formule explicite...)
Par ailleurs, cette expression de "solution double" ne signifie pas que la valeur en question "compte pour deux solutions" : (x-4)²=0 n'a qu'une et une seule solution, qui est x = 4.
Il serait, reconnais le, assez surprenant de dire : (x-4)² = 0 admet deux solutions, qui sont 4 et 4 ...
Cordialement,
Yzz 
salut
Par ailleurs, cette expression de "solution double" ne signifie pas que la valeur en question "compte pour deux solutions" : (x-4)²=0 n'a qu'une et une seule solution, qui est x = 4.
Il serait, reconnais le, assez surprenant de dire : (x-4)² = 0 admet deux solutions, qui sont 4 et 4 ...
d'accord et pas d'accord ....
(x - 4)^2 = (x - 4)(x - 4)
il y a deux facteurs donc deux solutions .... confondues .... donc une solution double ....

si f est un trinome (du second degré) alors l'équation f(x) = k admet 0 ou deux solutions .... ces deux solutions pouvant parfois être confondues ....

Salut carpediem 
Donc, si un de tes élèves te balance "(x-4)² = 0 admet deux solutions" , tu valides ?
je valide ... en faisant tout de même une réflexion ... du genre à savoir si 4 est différent de 4 ...
je préfère tout de même l'expression "une solution double" car 4 annule deux fois la fonction à l'expression "deux solutions confondues"
une remarque : on dit bien 4 est racine double du polynome ....

une autre remarque : je vois des élèves développer pour calculer un discriminant .... et ne pas trouver 4 ..... 



