Inscription / Connexion Nouveau Sujet
Nombre de triangle
Bonjour;
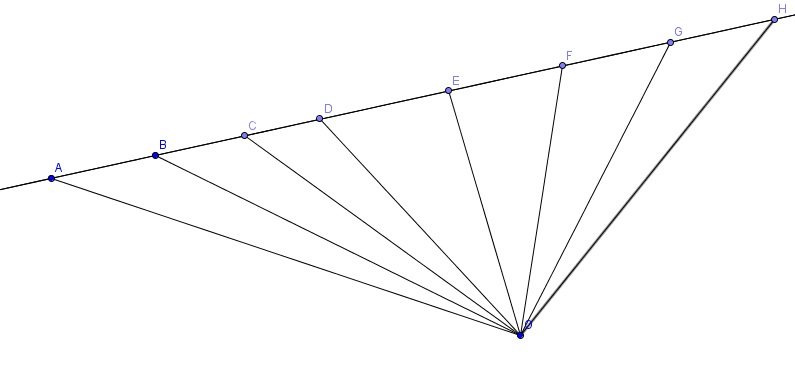
on place sur une droite 4 points et on relie par des segments au point O
On obtient et on peut nommer 6 triangles.
Si on place sur une droite n points que l'on relie tous au point O,combien pourra-t-on alors nommer de triangles?
Qui a une réponse et une explication? MERCI.
Bonjour, sépare les cas...
Tu as plusieurs manières de procéder, en voilà une assez pratique.
Prend le triangle le plus à gauche (OAB)
Combien y a t-il de triangles contenant OAB?
puis prend le triangle (OBC)
il faut compter les triangles contenant OBC, mais pas OAB (puisqu'ils ont déjà été compté)
combien en comptes tu?
Puis continue ainsi pour trouver le nombre total de triangles...
non,
fait comme je t'ai proposé:
triangle contenant OAB :
OAB, OAC, OAD,...,OAH
ça en fait 7.
ensuite...
Attention, tu as aussi compté les triangles contenant OAB
Tu as seulement OBC,OBD,OBE,...,OBH
Les triangles OAC,OAD,... contiennent effectivement OBC, mais comme ils contiennet aussi OAB, tu les as déjà comptés dans les 7 premiers...
OBC,OBD,OBE,OBF,OBG,OBH, pour moi ça fait 6 triangles...
Mais après c'est peut être une notion relative? 
Si on prend que A;B;C et D soit 4 points reliés à O,on a déja 6 tiangles
qui sont OAB;OBC;OCD;OAD;OAC et OBD
DONC avec plus de point , il doit y en avoir encore plus.Sur ton dessin il y en a plus que 6 mais comme toi , je cale!!
La je te demandais pas le nombre total de triangles de ma figure, je te demandais seulement le nombre de triangle contenant OBC et ne contenant pas OAB...
bonjour,
triangles élémentaires :
OAB/OBC/OCD/ODE/OEF/OFG/OGH--> 7
triangles constitués de 2 triangles élémentaires :
OAC/OBD/OCE/ODF/EOG/OFH-->6
triangles constitués de 3 triangles élémentaires :
OAD/OBE/OCF/ODG/OEH-->5
triangles constituéd de 4 triangles élémentaires :
AOE/BOF/COG/DOH-->4
triangles constituéd de 5 triangles élémentaires :
AOF/BOG/COH--> 3
triangles constitués de 6 triangles élémentaires :
AOG/BOH--> 2
triangles constitués de 7 triangles élémentaires :
AOH--> 1
La gwendolin a utiliser une autre approche...
Peut être que tu la comprendras mieux, tu comptes le nombre de triangles formés d'un seul petit triangle, puis le nombre de triangles formés de deux petits triangles...[sub][/sub]
Bonjour gwendolin;
donc cela ferait 28 triangles pour 8 point et 6 triangles pour 4 points et je pense qu'il faut chercher une formule qui donne la réponse de suite genre x points relié à un point commun = x triangle mais comment faire?
Tu trouves une suite:
si tu as n points, combien as tu de petits triangles?
et de triangles composes de deux petits triangles?
Genre pour 14 points il y en a;1 fait de 13 ;2 fait de 12;3 fait de 11;4 fait de 10;5 fait de 9;6 fait de 8;7 fait de 6;8 fait de 5;9 fait de 4;10 fait de 3;11 fait de 2;12 fait de 1 et 13 triangles élémentaires.
Mais peut on l'écrire sous la forme d'une formule?
Oui, mais je ne pense pas que cela puisses t'être demandé.
Demonstration:
Soit S = 1+2+3+...+n
2S = 1 + 2+ 3+ ...+n
+n+(n-1)+(n-2)+ ...+1
=(n+1)+(n+1)+(n+1)+...+(n+1)
=n(n+1)
donc S = n(n+1)/2
Bonjour;
peut tu vérifier stp ta formule avec l'énoncé de l'exercice pour voir si sa fonctionne.MERCI.