Bonjour,

Déterminer l'ensemble D des points d'affixe - 3/2 + iy avec ( y appartenant à R ).

Sauf erreur, il s'agit simplement de la droite parallèle à l'axe des ordonnées et coupant l'axe des abscisses en -3/2

Nicolas

Je vous remercie pour cette aide rapide et claire.

Il s'agissait juste d'une explication à donner et non un calcul.
J'ai pour mauvaises habitude d'essayer de répondre aux questions par un calcul alors que la réponse peut être littéraire.


J'aurais besoin d'un autre coup de pouce s'il vous plait.

Voilà, j'ai réussi à avancer dans l'exercice en répondant aux questions suivantes:

_ soit z1 = z + 1. Préciser la transformation géométrique.
J'ai dit qu'il s'agissait d'une translation.
_ même question pour z2 = 1 / z pour z différents de 0
J'ai réalisé la démonstration.
_ de même pour z3 = - z
J'y ai également répondu.

Mon soucis se trouve à cette question.

_ On me demande de déterminer l'ensemble des points M d'affixe Z = 1 - 1 / (z + 1) lorsque
z = - 3/2 + i y ( y appartenant aux réels R )

J'ai touvé une expression de la forme

Z = ( (3 + 4 y²) / (1 + 4 y²) )  +  ( (4 y) / (1 + 4 y²) )i

Je ne sais pas trop quoi en faire.


Pour la suite ça ira, je n'ai plus qu'à réprésenter ls points sur un repère.


Merci par avance de votre aide.


Julien
++

Bonjour;
julienb13,qu'as tu répondu pour la transformation ?

si z et z1 sont les affixes respectives de M et M1

OM * OM1 = 1 si et seulement si |z1| * |z|= 1 et Arg(z1) = - Arg(z) + 2 k PI


Propriété :

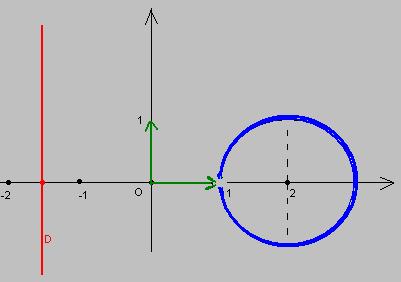
L'image d'une droite D ne passant pas par O par une inversion complexe est un cercle C privé du point O.

Nous sommes dans le cas où la droite D est parallèle à l'axe des ordonnés donc l'équation x = - 3/2 (dans le cas où y = 0)

z1 = x1 + w1 = 1 / z = 1 / a + ib  
......
z1 = [a / (a²+y²) - y/ (a²+y²) i]

puis

x1² + w1² = a² / (a²+y²) + y² / (a²+y²) = 1 / (a² + y²) = x1 / a

donc

x1² + w1² - x1/a = 0

x1² - 2 * 1/2a x² + 1/4a² + w1² = 1/4a²

( x1 - 1/2a )² + w1² = 1/4a²

Donc nous avons un cercle de centre O (1/2a = - 1/3)
et de rayon 1/2|a| = 1/3

Voilà, je pense que c'est ça.


Si vous pouvez m'aider sur la question:


_ On me demande de déterminer l'ensemble des points M d'affixe Z = 1 - 1 / (z + 1) lorsque
z = - 3/2 + i y ( y appartenant aux réels R )

J'ai touvé une expression de la forme

Z = ( (3 + 4 y²) / (1 + 4 y²) )  +  ( (4 y) / (1 + 4 y²) )i

Je ne sais pas trop quoi en faire.



Merci par avance.


Julien..

Bonsoir julienb13;
je voulais m'assurer de ta connaissance des propriétés des inversions planes en particulier ,comme tu l'as bien expliqué,que l'image par une inversion d'une droite ne passant pas par son pole est un cercle passant par le pole (privé du pole) et centré sur la pependiculaire (à la droite) passant par le pole.
Maintenant si on note l'ensemble qu'on te demande n'est autre que .
est la translation de vecteur elle va donc transformer en la droite paralléle .
est la composée de l'inversion de pole et de puissance et de la symétrie orthogonale d'axe et vu que est globalement invariante par (puisqu'elle est perpendiculaire à l'axe de ) on a que:
et on sait que est un cercle dont on connait 3 points , et tu vas sans doute me demander pourquoi et bien parce que le cercle unité étant invariant point par point par l'inversion ,son intersection avec qui est sera également invariante point par point par c'est à dire que
on doit facilement trouver qu'une equation cartésienne du cecle est c'est donc le cercle de centre et de rayon .
La symétrie de centre qu'est va transformer le cercle en le cercle de centre et de rayon .
Enfin,la translation tranforme ce denier en le cercle de centre et de rayon .
Conclusion:
La transformation transforme la droite en le cercle (privé du point d'affixe )

Sauf erreurs bien entendu