Inscription / Connexion Nouveau Sujet
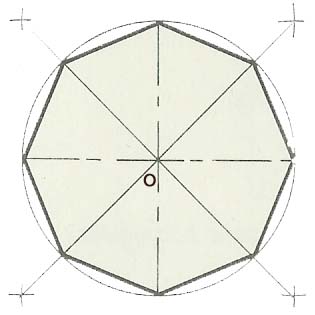
Octogone inscrit dans un cercle
Bonjour
Je m'appelle Robert et j'ai de la difficulté avec un petit problème
Le voici:
Je dois déterminer L'aire de l'octogone régulier de 8 cm de côté qui est inscrit dans un cercle
Je sais juste que c'est un octogone de 8 cm de coté
NB. Laisse toutes les traces de ta démarche, justifie tous tes calculs et illustre à l'aide du schéma les côtés et les angles utilisés dans ta démarche
svp aidez moi
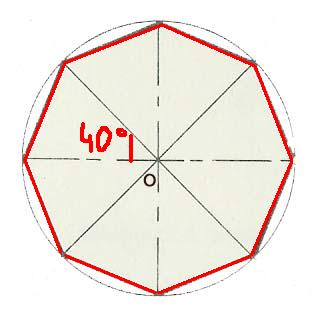
j'ai commencé par séparer mon octogone en 8 triangles où il y a un angle de 40 degré au centre (360/8)
doc, tu sais que chaque angle formé vaut 40° (vers le centre) donc tu sais aussi que le coté vaut 8 cm comme ceci :
tu traces la hauteur issue du sommet 0 de chaque triangle tu obtients donc 2 triangles rectangles, on va pouvoir y utiliser une des formules de trigonométrie afin de pouvoir y calculer le coté come ceci :
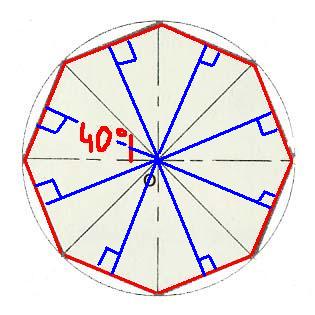
Maintenant on peut donc utiliser la tangente dans un des deux triangles rectangles qui composent un triangle isocéle 
donc :
Tan 45° =
=
on a ainsi :
coté adjacent =
= 8
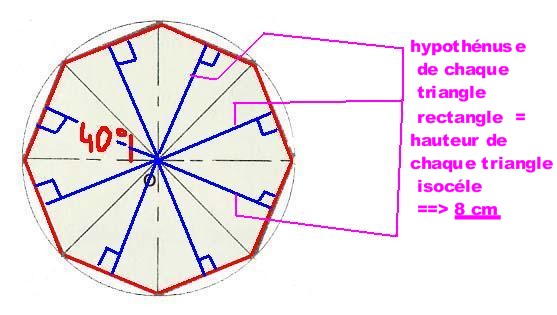
Ainsi l'hypothénuse vaut 8 m dans chaque petit triangle rectangle, on peut donc en conclure que la hauteur de chaque triangle isocéle vaut 8 cm
Comme ceci :
Edit Coll : LaTeX ne connaît pas (simplement) les accents 
Ainsi on peut donc calculer l'aire de chaque triangle isocéle (toujour une fois bien sur car tous les triangles isocéle sont égaux 
Donc :
Aire d'un triangle isocéle =
=
=
=
Donc on multiplie cette aire d'un triangle isocéle par 8 puisqu'il y en a 8, on donc :
32*8 = 256 cm²
Ainsi, l'aire totale de l'octogone est de 256 cm²
Voilà, j'espère que tu as bien comris mon raisonnement 
==> Ici tu as bien le "cheminement" des toutes les idées 
MAis lorsque tu fais:
Tan 45° =
=
on a ainsi :
coté adjacent =
= 8
C'est pas supposé etre tan de 22,5 ?
Salut a vous deux
J'ai une autre methode, la voici:
L'octogone est regulier, donc il est inscrit dans un cercle
Ma methode pour calculer l'aire serait la suivante:
Le cote de l'octogone vaut a, donc le carre c'est
Ensuite en bleu on a 4 triangles rectangles isocele dont on connait l'hypotenuse, d'ou les 2 autres cotes valent
Aire d'un triangle bleu:
Aire d'un rectangle vert:
Aire totale: 4 triangles, 4 rectangles, 1 carre, soit:


 2-1)
2-1)