Inscription / Connexion Nouveau Sujet
Olympiade de math 6
Bonjour à tous même principe , une question 20 encore de la géometrie avec plein de droite parallèle qui me font peur  Merci beaucoup !
Merci beaucoup !
l'énoncé :
Dans la figure ci-contre, les segments intérieurs au grand carré joignent un sommet au milieu d'un côté. Si l'aire du grand carré est 425 , quelle est celle du carré grisé ?
Déjà on sait que le coté du carré vaut 5 racine de 17  , ensuite on peut supposé que les droites atteignent le milieu du côté opposé , mais bon rien n'est sûr . J'ai essayé de faire : L'aire du carré - Aire des triangles auteur de la partie grisé , mais ces triangles se superposent par endroit ce qui fait que je dois enlever des morceaux à chaque fois et ça devient horrible
, ensuite on peut supposé que les droites atteignent le milieu du côté opposé , mais bon rien n'est sûr . J'ai essayé de faire : L'aire du carré - Aire des triangles auteur de la partie grisé , mais ces triangles se superposent par endroit ce qui fait que je dois enlever des morceaux à chaque fois et ça devient horrible  . Je suis bien conscient que cette manière de procédé est mauvaise , mais comment faire ? Utiliser thalès ? ça donne des valeurs bien horrible , je ne vois pas
. Je suis bien conscient que cette manière de procédé est mauvaise , mais comment faire ? Utiliser thalès ? ça donne des valeurs bien horrible , je ne vois pas 
Merci beaucoup 
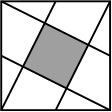
Petit double post désolé mais on ne peut pas éditer  En relisant l'énoncé on nous dit bien que les droites atteignent le milieu opposé , mais bon ça ne m'aide toujours pas ,
En relisant l'énoncé on nous dit bien que les droites atteignent le milieu opposé , mais bon ça ne m'aide toujours pas ,
et je voulais dire autour de la parti grisé , pas auteur 
Merci encore et désolé !
Salut
J'ai peut-être une idée
Tu vois les huit polygones blancs qui ont été créés par le traçage des droites parallèles
Quatre sont des triangles, et Quatre sont des trapèzes rectangles.
Tu peux peut être remarquer que si tu associes un trapèze rectangle avec un petit triangle rectangle (par rotation d'un petit triangle), tu obtiens un carré dont l'aire est égale au carré grisé
Ce n'est peut être pas ce qu'on te demande, mais tu peux exploiter cette piste et essayer de le justifier mathématiquement
bonsoir,
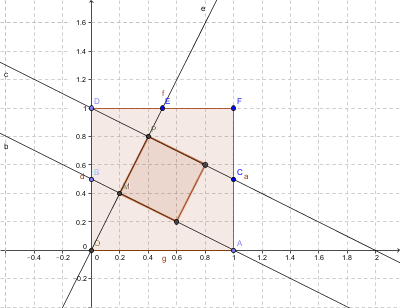
une autre idée : utiliser un repère.
le grand carré OAFD ==> on se place dans le repère (O, A, D),
soit C le milieu de AF, B le milieu de OD et E le milieu de FD,
exprime les equations des droites ((AB), (OE) et (DC),
puis le coordonnées des points P et M d'intersection de (OE) avec (DC) et (AB)
alors on peut calculer PM
enfin, une régle de proportionnalité donne le coefficient de réduction k de OA vers PM
==> appliquer k² à 425
Salut Leile
J'y avais pensé aussi mais j'avais peur que ce soit trop lourd, ou que ça ne corresponde pas au programme de 2de
bonsoir Zormuche
Si on travaille d'abord dans le carré de côté 1, les calculs sont plutôt faciles et correspondent à ce qu'on voit en seconde (voire 3ème) (coordonnées du milieu, repérage, équation de droites, distance entre deux points, coefficient de réduction, etc..).
mais voyons ce que FanDeMath en pensera.
Je quitte : bonne nuit.
salut
1/ entourer le carré de la figure par huit autres carrés identiques
2/ prolonger les droite tracées (et éventuellement rajouter les parallèles convenables)
3/ regarder et voir
Merci beaucoup  , vos méthodes sont vraiment jolies , et rien à voir avec ce que je voulais faire , finalement on devait même pas utilisé pythagore
, vos méthodes sont vraiment jolies , et rien à voir avec ce que je voulais faire , finalement on devait même pas utilisé pythagore  ,
,
Zormuche , je comprends ce que vous voulez me dire , je voyais déjà un peu ça , et que les petits triangles étaient identiques , mais je ne vois pas comment travailler là dessus en fait  enfin d'accord ça fait un carré ( d'ailleurs pourquoi égale à la partie grisé ? ) Ah en écrivant je pense que c'est parce que : En obtenant l'aire de ce nouveau carré et en faisant x5 on obtient l'aire du grand carré ( 425 ) , mais en fait même pas besoin de calculer
enfin d'accord ça fait un carré ( d'ailleurs pourquoi égale à la partie grisé ? ) Ah en écrivant je pense que c'est parce que : En obtenant l'aire de ce nouveau carré et en faisant x5 on obtient l'aire du grand carré ( 425 ) , mais en fait même pas besoin de calculer  425/5 = 85 voilà la réponse ( Je l'ai découvert en vous écrivant , mais je me base sur le fait que les carrés soient tous égaux , alors que j'en sais rien , pouvez vous m'expliquer ? Merci )
425/5 = 85 voilà la réponse ( Je l'ai découvert en vous écrivant , mais je me base sur le fait que les carrés soient tous égaux , alors que j'en sais rien , pouvez vous m'expliquer ? Merci )
Leile je trouve votre méthode tellement jolie  et très facile d'ailleurs , j'ai tout compris , mais j'ai juste peur de ne pas avoir assez de temps pour faire tout ça le jour des olympiades , sachant qu'il y a 30 questions , mais bon je réponds pas à tous de toute façon ( car je suis dans l'année inférieure , en Belgique plusieurs classe ont les même questions mais le seuil pour passer en demi final n'est pas le même ) , merci beaucoup en tout cas je vais essayer de le faire sur une feuille pour voir combien de temps ça me prend, merci beaucoup
et très facile d'ailleurs , j'ai tout compris , mais j'ai juste peur de ne pas avoir assez de temps pour faire tout ça le jour des olympiades , sachant qu'il y a 30 questions , mais bon je réponds pas à tous de toute façon ( car je suis dans l'année inférieure , en Belgique plusieurs classe ont les même questions mais le seuil pour passer en demi final n'est pas le même ) , merci beaucoup en tout cas je vais essayer de le faire sur une feuille pour voir combien de temps ça me prend, merci beaucoup 
Bonjour,
il me semble que la méthode suivante n'a pas été explicitée :
en réponse directe à "mais ces triangles se superposent par endroit"
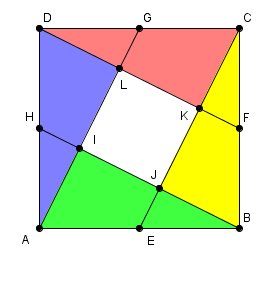
ces triangles là ne se superposent pas !
le calcul de leur aire revient à calculer "des trucs" associés à la hauteur (CK) d'un triangle rectangle (DCF) dont on connait les deux côtés de l'angle droit
formule donnant la hauteur d'un triangle rectangle (elle sst suffisamment jolie pour la retenir)
1/CK² = 1/CD² + 1/CF²
formule donnant les segments déterminés par le pied de la hauteur :
DC² = DK.DF
ces formules (hors cours officiel) sont commodes à retenir avec d'autres du même genre concernant les triangles rectangles pour s'attaquer à des questions d'Olympiades
à l'époque (les années 60) il y avait tout un paquet de formules en plus de Pythagore pour les triangles rectangles dans le livre de maths de seconde ou de première (première = révisions de seconde sur ce sujet là)
de plus cette figure et ce découpage là amène "naturellement" au découpage de Zormuche/Lake qui permet de simplifier le calcul à presque rien.
voire même sans les formules du tout :
j'appelle a le côté du carré ABCD
Pythagore dixit
l'aire de CDF (aire d'un triangle rectangle)
le triangle CDK est semblable à CDF (vu qu'ils ont leurs angles égaux, les triangles semblables sont revenus dans le programme de cours)
le rapport de réduction donnant CDK est
le rapport des aires est le carré de ça c'est à dire que l'aire de CDK
comme il y a 4 triangles identiques à CDK dans ma figure, ce qui reste (le carré cherché) a donc pour aire a² - 4a²/5 = a²/5, le 1/5 de l'aire de ABCD.
salut
1/ entourer le carré de la figure par huit autres carrés identiques
2/ prolonger les droite tracées (et éventuellement rajouter les parallèles convenables)
3/ regarder et voir
(presque) exactement ce que je disais ...


Par la géométrie analytique, c'est quasi immédiat. (mais moins joli ?)
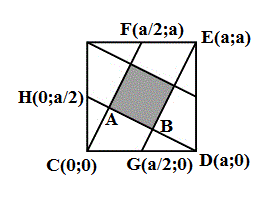
A est le point de rencontre de (CF) et de (HD)
Résoudre le système :
y=2x
y=-x/2 - a
--> A(a/5 ; 2a/5)
-----
B est le point de rencontre de (GE) et de (HD)
Résoudre le système :
y=2x-a
y=-x/2 - a
--> B(3a/5 ; a/5)
-----
AB² = (2a/5)² + (a/5)² = a²/5
Or a² = 425
--> AB² = 425/5 = 85
L'aire du carré grisé est 85 unités de mesure d'aire.

Ah oui très beaau vos 2 méthodes , qui sont bien différentes d'ailleurs , les deux sont simples très facile à faire , même si je pense que celle de J-P est un peu plus longue , mais bon je n'ai jamais fait de géometrie analytique , donc je suis un peu lent je l'avoue :p En tout cas très belle technique à tous les deux , je sais maintenant faire ce genre d'exercice de plusieurs façon ( J'ai trouvé un exercice avec le même dessin , ou on demandait le rapport de périmètre , j'ai tout de suite trouvé grâce à vous  merci ! )
merci ! )
bonsoir FanDeMath,
juste un petit complément d'info : la méthode qu'a proposée J-P est proche de la mienne, je suppose que tu l'as vu ; J-P pose le coté du carré = a, alors que perso, je pose le coté du carré = 1.
Dans les deux cas, l'équation des droites est quasi immédiate..
C'est vrai que par rapport aux autres propositions (où les schémas sont explicites), il y a plus de calculs !

Bonne nuit !