Inscription / Connexion Nouveau Sujet
Optimisation - utilisation des dérivées
J'ai absolument besoin de votre aide pour l'exercice suivant !!
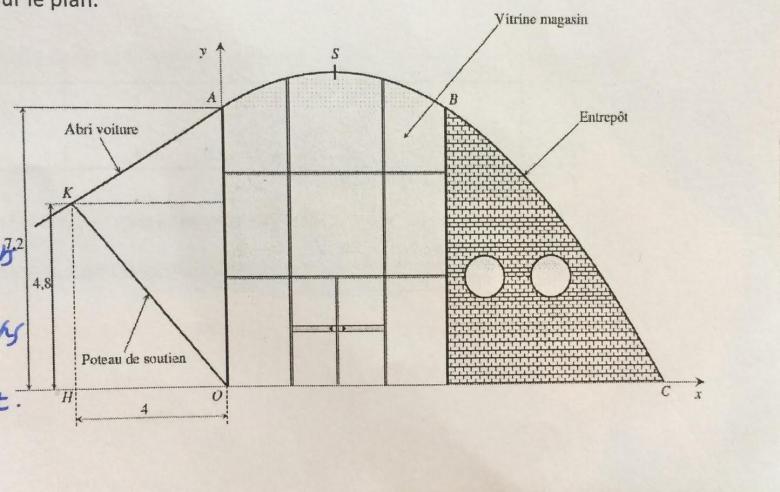
Le propriétaire d'un magasin souhaite proposer un abri couvert pour les voitures de ses clients. Il voudrait prolonger le toit de son magasin pour le moins original puisqu'il s'agit d'un arc de parabole. Pour ne rien perdre de cette esthétique parfaite, une des principales exigences est la continuité visuelle de la toiture.
Détermine une équation de la tangente à la toiture existante au point A et vérifie que le poteau de soutien se positionnera exactement à l'endroit souhaité sur le plan.
Dans le repère donné, les points A, S et B ont pour coordonnées respectives A ( 0 ; 7,2 ) , S (3 ; 8,1 ) et B ( 6 ; 7,2 ).
Bonjour (ça se dit parfois, chez les gens civilisés).
Donne un énoncé complet, tes pistes de recherche...
Je mesure la distance K-A grâce au théorème de pythagore : 3,5.
Ensuite je trouve la pente : quand j'avance de 4 je monte de 2,4 donc j'ai une pente de 0,6.
Mais ensuite je n'y vois plus trop claire..
Je dois parvenir à dériver l'équation de ma fonction mais comment trouve t'on cette équation?
Utilise ces coordonnées pour trouver l'équation de la parabole :
f(x) = ax²+bx+c
Elle passe par A , donc f(0) = 7,2 , donc a*0²+b*0+c = 7,2 donc c = 7,2
Fais pareil avec S et B , ou utilise aussi le fait que S est un sommet (dérivée = 0)
viodegruben, tu as intérêt à fermer ton autre compte si tu veux pouvoir revenir poster sur notre site
le multicompte est interdit

(modérateur)