Inscription / Connexion Nouveau Sujet
Parabole.
On considère la parabole P d'équation :
y = -4x² + 4x - 1
1. Factoriser l'équation.
Je trouve y = -(2x-1)²
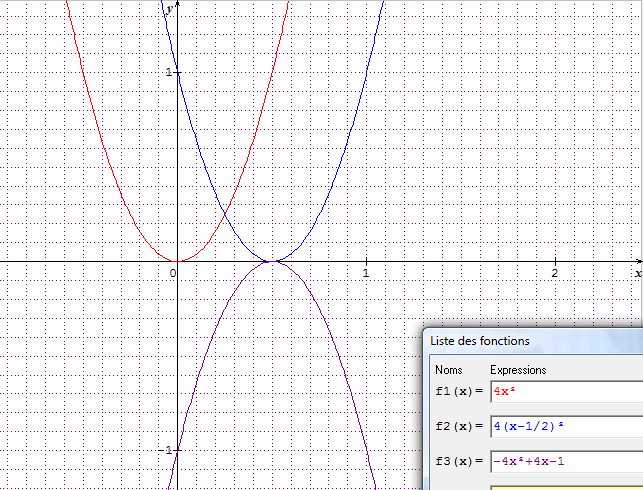
2. En utilisant les fonctions associées, indiquer les transformations qui permettent d'obtenir la parabole P à partir de la parabole d'équation y=4x².
3. Construire la parabole P.
4. Dresser le tableau de variation de la fonction :
f : x => -4x² + 4x - 1
J'aurais besoin d'aide à partir de la 2 ^^"
Bonjour
En notant et
On a
Donc on obtient (Cg) à partir de (Cf) par la translation de vecteur (1/2) suivi de la réflexion d'axe (Ox).
suivi de la réflexion d'axe (Ox).
sauf erreur

J'ai pas compris... On me demande la parabole de -4x² + 4x - 1 à partir de 4x²...
Et j'ai pas compris ce que t'as fait en fait.
Comme l'énoncé dit
En utilisant les fonctions associées
Puis j'ai observé que
pour f(x-1/2), on a une translation de vecteur (1/2)

ensuite on prend -f(x-1/2) donc la symétrie orthogonale d'axe (Ox)
Vu par "sinequanon" :