Inscription / Connexion Nouveau Sujet
Parabole d'équation
Bonjour, j'aurais besoin d'aide sur cette exo:
Construction de la parabole d'équation p(x) = x² +4x +1
1) Vérifier que x²+4x+1 = (x+2)² - 3
2) Soit les fonctions f:x-->x², g:x-->f(x+2) et h:x--> g(x)-3 définies sur R
Vérifier que h(x)=x²+4x+1
3) Cf, Cg, Ch sont les courbes représentatives des fonctions f,g et h dans un repère othonormal
a) Par quelle transformation géométrique Cg est-elle l'image de Cf ?
b) Par quelle transformation géométrique Ch est-elle l'image de Cg ?
4) Construire les courbes
5) Par quelle transformation géométrique, Ch est-elle l'image de Cf ?
6) Résoudre graphiquement les équations h(x) = 1, h(x) = -2 et h(x) = 6
7) Vérifier en résolvant algébriquement ces équations
J'ai fait la question 1)
x²+4x+1=(x+2)²-3
x²+4x+1=(x²+2x*2²+2)-3
x²+4x+1=(x²+4x+2²)-3
x²+4x+1=(x²+4x+4)-3
x²+4x+1=x²+4x+1
Mais je bloque sur les autres
Merci Merci d'avance
Bonsoir,
2) Ce n'est tout simplement qu'une composition de fonctions !!
Comment définis-tu les fonctions f,g et h ?
Ah et j'ai eu une idée aussi pour la 3,4,5
3) On se place dans un repère orthonormé (0,vecteur i,vecteur j)
a. Translation de vecteur -2i
b. Translation de vecteur -3j
4. Voir image
5. Translation de vecteur -2i-3j
Par contre la 6 et la 7 je ne trouve pas pour le moment
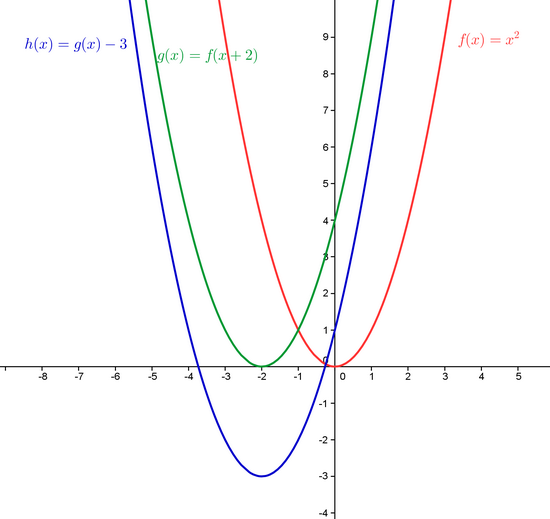
C'est pas mal !!
6) On te demande de résoudre graphiquement les équations h(x)=1, h(x)=-2 et h(x)=6.
Pour résoudre graphiquement h(x)=1, commences par tracer la droite horizontale d'équation y=1.
Les solutions sont les abscisses des points d'intersection de la courbe h (que tu as tracée en bleu) et de la droite d'équation y=1.
Les 2 autres équations se traitent de la même manière.
7) Cette fois ci, c'est par le calcul :
h(x)=1
(x-2)² - 3 = 1
Tu fais passer à gauche le "1" : (x-2)² - 3 - 1 = 0 => (x-2)²-4 = 0.
Et là tu reconnais une identité remarquable a²-b².
Les 2 autres se traitent pareillement.


