Inscription / Connexion Nouveau Sujet
Paramètres dans une hyperbole
Bonjour,
J'ai une question concernant les coniques, en particulier l'hyperbole.
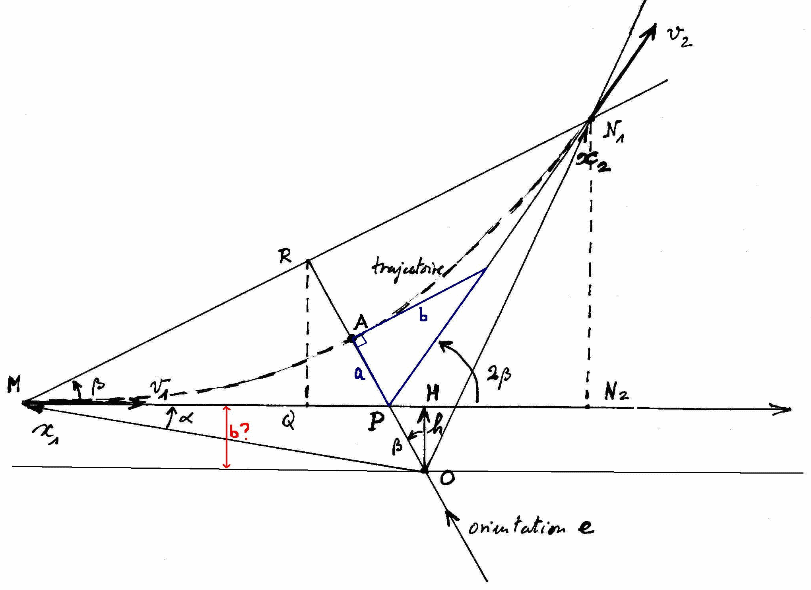
O étant le foyer, on a la définition des demi-grand/petit axes a et b (en bleu). Or dans l'expérience de Rutherford, on appelle souvent le paramètre d'impact b (en rouge). Ces deux longueurs b sont effet égales (d'après mon cours de phi) et on peut facilement trouver la cotangente de la déviation cotan(2
) en travaillant dans le triangle bleu.
Ma question est : comment montrer que ces deux longueurs sont égales ? J'ai essayé de bidouiller mais j'ai pas trouvé.
Merci
bonsoir,
Figure trop imprécise ou non commentée pour avoir une réponse
Attention ton point O n'est pas un foyer de ton hyperbole, l'un des foyer est sur la demi-droite [AR) O est peut-être le centre de symétrie de l'hyperbole ? à toi de le dire , de même a n'est pas le demi-grand axe,
Définis bien ton hyperbole, où est le foyer ? valeur de l'excentricité ?, Directrice?
ou tout simplement équation dans le repère défini par le centre et les axes.
Question: Par rapport à ton hyperbole comment définis-tu le point O, à priori N1P et MP sont des tangentes.
C'est un schéma classique de la trajectoire hyperbolique de l'électron dans l'expérience de Rutherford, schéma connu de tous les taupins, c'est pour ça que je n'ai pas commenté la figure. Pour l'imprécision, il faut avouer que tracer une vraie hyperbole à la main n'est pas chose aisée, et donc les deux distances b n'ont pas l'air égales, mea culpa.
Je vais détailler alors:
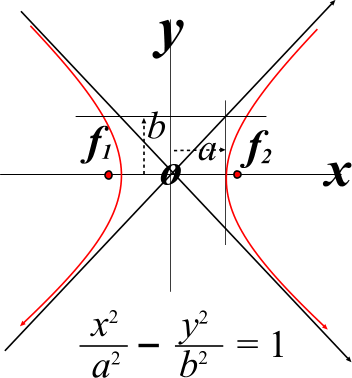
Ce que j'ai représenté c'est une des deux branches de l'hyperbole. Si on prend le schéma simple ci-dessous (pris d'internet, source http://www.asc-csa.gc.ca/fra/educateurs/ressources/orbites/math_orbite.asp) , alors:
- la trajectoire en pointillé du schéma du 1er post (que je vais appeler schéma 1) est la branche gauche du schéma ci-dessous (nommé schéma 2)
- le point O du schéma 1 est le point f2 du schéma 2.
- le point P du schéma 1 est le point O du schéma 2
- la droite (RO) du schéma 1 est la droite (Ox) du schéma 2
Ainsi dans le schéma 1:
- (N1P) et (MP) sont les deux asymptotes (dirigées par v1 et v2), elles se coupent en P centre de symétrie
- les droites OM et ON1 ne servent à rien il est vrai, de même que le point R et la droite (MRN1), c'est peut-être ça qui prête à confusion
Les distances a et b sont alors les mêmes dans les deux schémas.
Bonjour,
Le graphique ci-dessous représente, rapportée à ses axes, l'hyperbole d'équation et son asymptote d'équation
.
La distance entre les sommets S1 et S2 est égale à 2a, et la distance séparant les foyers F1 et F2 est .
Si j'ai bien compris, tu veux prouver que F2H = b.
Mais les triangles rectangles OHF2 et OS2K sont égaux (isométriques), car ils ont deux angles égaux et OK = OF2 = c.
Donc HS2 = KS2 = b.
Annuler
connectez vous
géométrie en post-bac