Inscription / Connexion Nouveau Sujet
Pb sur les suites: construction des Triangles equilateraux
Bonjours:
mon pb est le suivant
T1 est un Triangle equila de coté 1
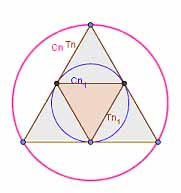
On considere la suite de triangles et la suite de cercles ainsi definies:
Pour n>1, Tn+1 est le triangle dont les sommets sont les milieux des cotes du triangle Tn et Cn est le cercle circonscrit au triangle Tn
1) Montrer que si Tn est equilatere alors Tn+1 l'est aussi. On peut deduire de proche en proche que tous les Tn sont équilatéraux
2) Pour n>1 on note an la longueur du cote du triangle Tn
a) Exprimer an+1 en fonction de an
b) Exprimer an en fonction de n
3) Pour n>1 on note rn le rayon du cercle Cn
a) exprimer rn en fonction de an
b) demontrer que la suite (rn) n>1 est geometrique
Bonjour.
Il te manque quelques vieux souvenirs des années antérieures.
1°) le théorème de la droite des milieux
2°) la hauteur d'un triangle équilatéral de côté "a" mesure :.
3°) le centre de gravité est situé au 2/3 de la médiane à partir du sommet.
Reprends ton exercice avec ces précisions, tu dois mieux t'en sortir.
Cordialement RR.


