Inscription / Connexion Nouveau Sujet
Pentagone régulier
Bonjour a tous, voila j'ai un dm à rendre et je bloque.
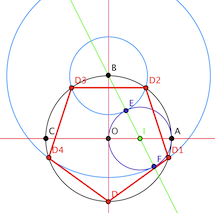
On nous demande tout d'abord de construire un pentagone régulier (inscrit dans un cercle). Voir la photo jointe.
Ensuite on nous dit :
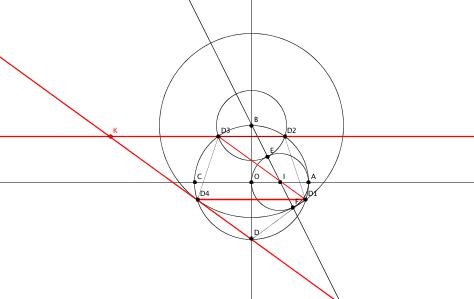
1. Prolonger (D2D3) et (DD4). Ces deux droites se coupent en K. Tracer [D1D3] et [D1D4].
2. On note c la dimension du côté de l'hexagone (quel hexagone ?? je n'arrive pas à déterminer où il est) et d la dimension de chaque diagonale (sans hexagone je peux pas les voir). Calculer d/c.
J'aimerai donc avoir de l'aide pour voir l'hexagone sur la figure et enfin quand on doit calculer d/c, sachant que le rayon du cercle C (le noir) est un rayon d'unité quelconque. Comment faire ??
Merci d'avoir pris le temps de me lire. En espérant que vous puissiez m'aider.
Bonjour,
je pense qu'il y a une petite erreur dans l'énoncé et qu'il faut remplacer hexagone par pentagone .
Pour les calculs demandés , il faut prendre r = 1 . c'est ce qu'on appelle le rayon unité sans se soucier si c'est 1 m , 1 cm , 1 mm , ...
Cordialement
Bonjour fm_31, je me suis également dit qu'il y avait une erreur mais pourquoi prolonger (D2d3) et (DD4) si il suffit juste de calculer les côtés du pentagone qu'on a déjà avant de répondre a la question 1 ?
Après avoir fait les constructions qui correspondent à la question 1 (voir photo ci-jointe), on obtient 6 sommets mais impossible de discerner l'hexagone.
En ce qui concerne la réponse 2 merci de votre aide !
Merci pour votre réponse !
Ce qui est demandé , c'est le rapport d/c . Pour cela il faut bien calculer (exprimer) d et c (en fonction de r qu'on remplacera par sa valeur 1).
Il se peut que le point K soit utile pour ces calculs mais je n'ai pas vérifié .
Cordialement
En effet , après avoir remarqué que les triangles DD4D1 et D3KD sont semblables , tu peux écrire :
D1D4 / DD4 = (KD4 + D4D) / DD3
d/c = (d+c) / d
= 1 + c/d en multipliant les 2 membres par d/c
(d/c)2 = d/c + 1
(d/c)2 - d/c - 1 = 0 équation du second degré qu'il suffit de résoudre pour trouver d/c = 
Cordialement
(d/c)² - d/c - 1 = 0
(d/c-1/2)² - 5/4 = 0
(d/c-1/2)² - (√5/2)² = 0
[ (d/c-1/2) - (√5/2) ] [ (d/c-1/2) + (√5/2) ] =0
(d/c - 1/2-√5/2) (d/c - 1/2+√5/2) =0
donc d/c = 1/2+√5/2 ou d/c = 1/2-√5/2
C'est ça ?
Oui c'est bien cela . Comme d/c doit être > 0 , on ne retient que la première racine soit (1+ 5) / 2 (soit la valeur du nombre d'or) .
5) / 2 (soit la valeur du nombre d'or) .
La stratégie utilisée pour trouver les racines (forme canonique) n'est peut-être pas la plus rapide .
x2 - x - 1 = 0 entraine x = (1 
 (1 + 4)) / 2 soit x = (1 +
(1 + 4)) / 2 soit x = (1 +  5) / 2
5) / 2
Cordialement
D'accord merci beaucoup pour votre aide ! J'ai compris le raisonnement mais je ne vois pas bien pourquoi on peut écrire D1D4 / DD4 = (KD4 + D4D) / DD3. Comment dire que les deux triangles sont semblables ?
Il suffit de montrer qu'ils ont leurs 3 angles égaux puis d'appliquer le théorème de Thalès .
Cordialement
pour le triangle DD4D1 ok ! pour le triangle KD3D, on a l'angle D, mais pas les autres. On ne peut également pas montrer que c'est un triangle isocèle ne connaissant pas les longueurs.
Il y a plusieurs façon de démontrer l'égalité des angles . Par exemple en remarquant que le quadrilatère D1D3KD4 est un losange on en déduit l'égalité des angles et aussi le fait que les triangles sont isocèles .
Cordialement


