Inscription / Connexion Nouveau Sujet
Pentagone régulier dans un cercle trigonométrique
Bonjour, j'ai un DM à faire est je bloc, voilà l'énoncer:
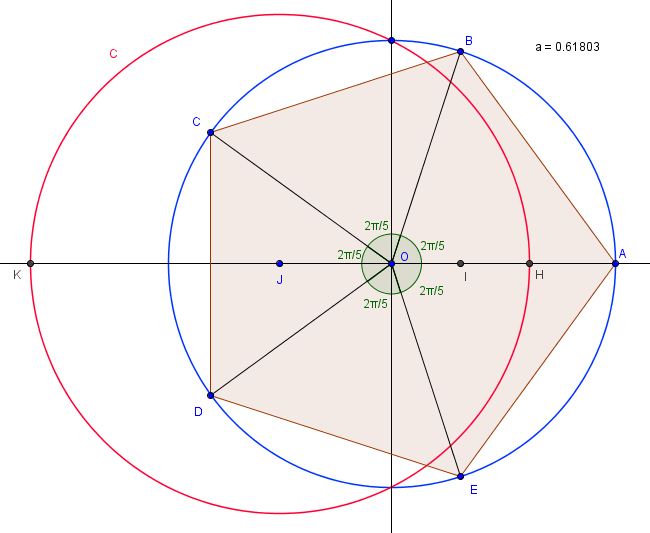
Sur le cercle trigonométrique, on place les points:
A (1;0) B (cos 2
/5 ; sin 2/5) C (cos 4/5 ; sin 4/5) D (cos 6/5 ; sin 6/5) E (cos 8/5 ; sin 8/5)
1.a) Expliquer pourquoi ABCDE est un pentagone régulier.
b) Montrer que les points B et E d'une part et C et D d'autre part sont symétriques par rapport à l'axe (x'x).
2. En utilisant que O est l'isobarycentre du pentagone ABCDE, montrer que 1+2cos2/5+2cos4/5)=0
3.a) En utilisant que cos2a=2cos2a-1, montrer que cos2/5 est une solution de l'équation (E):4X2+2X-1=0
b) En déduire la valeur exacte de cos2/5.
4.a) Soit C le cercle centré au point J(-1/2;0) et passant par le point de coordonnée (0;1). Déterminer une équation de C.
b) Le cercle C coupe l'axe des abscisses en deux points H et K et soit H le point d'intersection dont l'abscisse a est positive. Déterminer les abscisses des points H et K et vérifier que a=2cos2/5.
c) Soit I le milieu de [OH]. Déterminer l'abscisse de I.
Merci d'avance pour vos réponse !
1.a. Les cinq triangles AOB, BOC, COD, DOE, EOA sont isocèles avec le même angle au sommet (2pi/5) et la même longueur (1) pour les deux côtés de même longueur. Ces 5 triangles sont donc superposables. Donc AB=BC=CD=DE=EA. Le pentagone est régulier.
2.
O est l'isobarycentre du pentagone ABCDE donc :
Traduisons-le en coordonnées :
On n'utilise que la première relation, avec les abscisses ("x") :
3.a. On a montré à la question précédente que :
On utilise l'indice donné par l'énoncé :
Donc est solution de l'équation 4X²+2X-1=0.
La trigonométrie est un sujet que je ne métrise pas très bien. J'ai donc fais des recherches, j'ai regarder ave des potes, mais même eux ne trouve pas la réponse à la question 4. Vous en pensez quoi ?
Et par quel calcul en 3.b trouve tu -1+
5/4 et -1-5/4 ?
C'est avec le delta je pense ! mais pourrais tu détailler le calcul stp ?
3.b. C'est en effet grâce au discriminant qu'on trouves les solutions de l'équation. Je te laisse le faire. C'est une pure question de cours.
4.a. Un point M de coordonnées (x;y) appartient au cercle de centre O(x0;y0) et de rayon r si et seulement si :
(x-x0)² + (y-y0)² = r²
C'est une conséquence du théorème de Pythagore.
Il te faut maintenant adapter cela à notre exercice.
Excuse moi d'insister mais pour le discriminent de la question 3.b, je suis rester 1heure dessus hier soir sans trouvé. tu pourrais me donner un petit coup de pouce ?
Moi je pars de du résultat trouvé en 2 et en 3.a ( j'ai fais deux calcul différents pour essayer) mais je n'y arrive pas. J'ai appliquer la règle du discriminent, mais rien y fait ! le résultat ne veux pas apparaitre ! Pourrais tu me montrer quel calcul tu fais stp !
3.b. Il s'agit de résoudre l'équation 4X²+2X-1=0 avec la méthode vue en cours pour résoudre les équations du second degré (discriminant, etc...).
Montre tes calculs, et je le corrigerai. Pas de souci.
Donc si je comprend bien, on par de 4X2+2X-1=0 et on utilise le discriminent ?
Ca fait donc (2X)2-4
4X2?
En effet, dans notre cas, la formule est: 4X2+2X-1=0.
a=4
b=2
c=1
La formule du discriminent étant: b2-4ac, on a:
4-44
c étant égale a 1, on le compte pas dans la formule. Ca nous fait donc:
4-16 = -12
Delta étant inférieur à 0, il n'y a pas de racine réelle.
Alors je me suis tromper où ?
Je n'apprécie pas la façon dont tu me parles.
Je t'ai donné tout cuit la réponse à de nombreuses questions.
Si "cela fait deux jours qu'on est dessus", c'est parce que tu ne fais aucun effort.
4X² + 2X - 1 = 0
aX² + bX + c = 0
a = 4
b = 2
c = -1 <---------------------
Est-ce si compliqué ?
Ceci est mon dernier message.
Annuler
connectez vous