bonsoir

x=0 =>
a)soit t=-1 et y=-2 => il ne te reste plus qu'à calculer la tangente en (0;-2)
b)soit t tends vers + ou - l'infini => y=0 => le point O est asymptotique
reste à savoir si on a le droit de parler de tgte en un point non défini

A vérifier
.

un lien pour les tangentes : http://c.caignaert.free.fr/chapitre15/node1.html
.

salut mikayaou,pour calculer la tangente en (0,-2),je fais ça avec les dérivées??Et pour le b) la concavité,c'est juste dire que O est asymptotique...??
Merci de tes réponses
(PS: je connais ce lien, maisje n'arrive à appliquer à ma courbe??)

en fait, l'intégrale du cours de christophe caignaert est très bien fait : http://c.caignaert.free.fr/chapitre15.pdf

Enjoy!
.

Je dois, malheureusement, laisser la main

bon courage (pleins d'aideurs attendent pour t'aider...)
.

merci mikayaou pour tes réponses,bone fin de soirée et merci aussi pour le cours

Rebonjour à tous, je fais remonter mon post, en vous reposant les questions de maniere un peu plus claire:
1)La droite affine d'équation x=0 dans les coordonnées usuelle est-elle une tangente à la courbe C
2)Déterminer les éventuelles branches infinies de C
3)Etudier la concavité de C en précisant ses éventuelles point d'inflexion.
4)le dessin(ça ok grace à ça:).

Pour la question 1) dire que x=0 =>t=-1=>y=-2 mais aprés??
Pour la 2) je suupose qu'il y une branche infinie en 0 mais je ne sais pas comment le justifier(lim f=+-oo??) et coment l'étudier
Et pour la concavite,est-ce qu'il suffit de dire que o est asymptotique...??
Merci d'avance à tous ceux qui pourront m'aider.

bonjour robby3

hormis te fournir la courbe avec SQN, je laisse la main à plus compétent pour bien t'expliquer
.

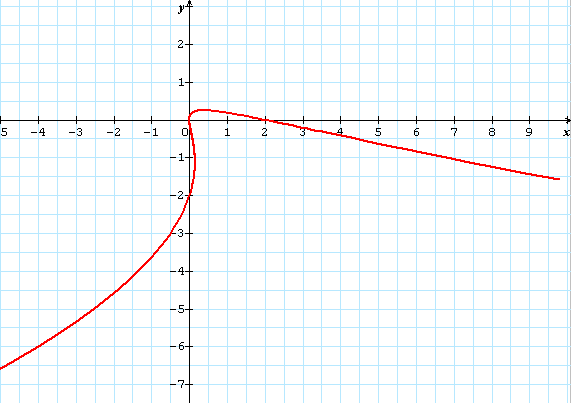
Merci à toi mikayaou,ce trés joli dessin me permet de confirmer que x=0 n'est pas tangente à C...mais comment le démontrer??(la courbe n'espas défini en (0,0) donc la courbe ne passe pas en (0,0)...
Merci à ceux qui m'aideront et déja un grand merci à Mikayaou.

pour moi, O est un point asymptotique quand |t| tend vers l'infini

qu'il y ait des demi-tangentes verticales, elles ne seront qu'asymptotiques...

A vérifier
.

mais qu'est ce que ça signifie mathématiquement que O est asymptotique??ça veut dire que lim qd t->|t| f(x,y)=0??

Tout est dans le cours de CC ! calcule les dérivées : x'(-1)=-1, y'(-1)=-3 sauf erreur, d'où au point de paramètre t=-1, une tangente dirigée par donc pas d'équation x=0...

ça signifie, comme l'indique l'étymologie d'asymptotique :

http://atilf.atilf.fr/dendien/scripts/tlfiv5/advanced.exe?8;s=618395655;

qu'il ne peut être atteint mais qu'il s'en rapproche interminablement.
.

merci lafol de prendre la suite
.

je ne voulais pas te chasser, mikayaou !

Avec plaisir, lafol

j'avais bien aimé ton intervention, très imagée, l'autre jour :

...si on allume des lampes de plusieurs côtés du même objet, on diminue les zones d'ombre ...
.

...qui s'applique tout à fait ici

( pour ma part, je ne suis pas une lumière )
.

salut lafol, ok pour la tangente, je pensais qu'il fallait faire avec les dérivées mais je n'étais pas sur du tout...Donc pour les branches infinies, comme lim x(t)=lim(y(t))=+- oo,si je fais (y/x)(t) et que je regarde la limite, ça donne rien, donc il n'y aurait pas de branches infinies?? meme avec un trés bon cours,celui que mikayaou m'a passé, je ne vois pas bien comment étudier la concavité??)

tu es marrant, toi, avec tes limites ! tu les calcules quand t tend vers quoi ? Si tu ne précises pas, ça n'a guère de sens !
J'imagine que c'est quand t tend vers 0 que tu trouves ces limites infinies ?
Pour moi, la limite en 0 de y/x est 0, non ? "ça donne rien" : tu veux dire par là que ça donne 0 ? Mais ce n'est pas rien, 0 , mon bon monsieur ! (excuse si t'es une dame !) ça veut dire direction asymptotique horizontale, donc branche parabolique dans la direction de (Ox) !

Clique là et essaye de comprendre ! il y a même des exemples développés !

Moi, je dois quitter l'île !

alors,oui je suis bien un monsieur,la limite c'est bien en 0 et et la lilite de y/x qd t->0 c'est bien 0,donc branche parabolique de direction (Ox),ça OK.
Pour la concavité, je voudrais juste savoir ce que je suis censé faire quand on me dit "étudier la concavité de la courbe?"
Merci encore de votre patience et de vos réponses

en deux mots et je pars! chercher les éventuelles inflexions (avec un déterminant regarde le lien qu'on t'a passé c'est expliqué !) et regarder si la courbe est "au dessus" ou "en dessous" de ses tangentes (sachant qu'elle les traverse pour changer de côté justement aux points d'inflexion)