2) 2 divise x et y donc 3 n + 1 0 modulo 2 donc n 1 modulo 2 alors n = 2 k + 1
x = 6 k + 4 = 2 (3 k + 2)
y = 10 k + 4 = 2 (5 k + 2)
5 (3 k + 2) - 3 (5 k + 2) = 4 donc le PGCD de (3 k + 2) et (5 k + 2) divise 4 donc est égal à 1; 2 ou 4
Ces deux nombres sont premiers entre eux si et seulement si 2 ne divise pas (3 k + 2) et (5 k + 2) donc si et seulement si k est impair soit k = 2 q + 1
donc x = 2 (6 q + 5) et y = 2 (10 q + 7) q entier relatif.
soit si n = 4 q + 3, x = 12 q + 10 et y = 20 q + 7 et PGCD(x ; y) = 2


3) 4 divise x et y donc 3 n + 1 0 modulo 4 donc - n + 1 0 modulo 4 alors n = 4 k + 1
x = 12 k + 4 = 4 (3 k + 1)
y = 20 k + 4 = 4 (5 k + 1)
5 (3 k + 1) - 3 (5 k + 1) = 2 donc le PGCD de (3 k + 1) et (5 k + 1) divise 2 donc est égal à 1 ou 2
Ces deux nombres sont premiers entre eux si et seulement si 2 ne divise pas (3 k + 1) et (5 k + 1) donc si et seulement si k est pair soit k = 2 q
donc x = 4 (6 q + 1) et y = 4 (10 q + 1) q entier relatif.
soit si n = 4 q + 1, x = 24 q + 4 et y = 20 q + 4 et PGCD(x ; y) = 2

4. 8 divise x et y donc 3 n + 1 0 modulo 8 donc 3 (3 n + 1) 0 modulo 8 donc n + 3 0 modulo 8 soit n 5 modulo 8 alors n = 8 k + 5
x = 24 k + 16 = 8 (3 k + 2)
y = 40 k + 24 = 8 (5 k + 3)
5 (3 k + 2) - 3 (5 k + 3) = 1 donc le PGCD de (3 k + 2) et (5 k + 3) = 1
Ces deux nombres sont premiers entre eux
soit n = 8 q + 5, x = 24 k + 16 et y = 40 k + 24 et PGCD(x ; y) = 8

En divisant n par 8 : n = 8 q + r
n = 8 q + 1 ou n = 8 q + 5 n = 4 Q + 1
n = 8 q + 1 ou n = 8 q + 5 PGCD (x ; y) = 2

n = 8 q + 3 ou n = 8 q + 7 n = 4 Q + 3
n = 8 q + 3 ou n = 8 q + 7 PGCD (x ; y) = 4

Les autres cas :
n  = 8 q ou n = 8 q + 2 ou n = 8 q + 4 ou n = 8 q + 6 n pair
n pair PGCD (x ; y) = 1

salut
merci cherchell pour votre aide
votre correction est très clair
j aime bien te contacter par email voici mon adresse mathsnour2015@gmail.com
j ai une autre façon mais a l aide d un tableau si possible de me  vérifier ma méthode  
merci beaucoup

salut
merci cherchell pour votre aide
votre correction est très clair
j aime bien te contacter par email voici mon adresse mathsnour2015@gmail.com
j ai une autre façon mais a l aide d un tableau si possible de me  vérifier ma méthode  
merci beaucoup

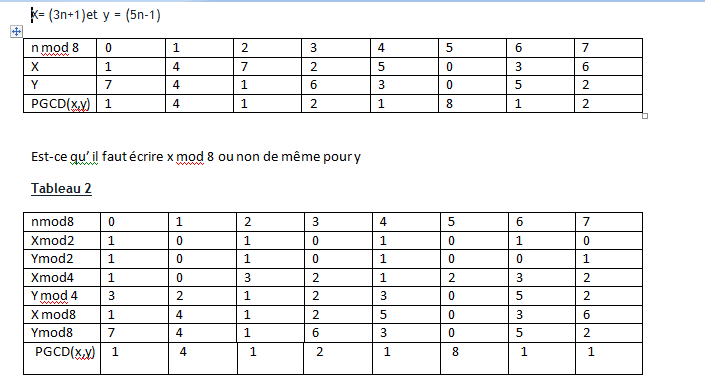
salut Cherchell

merci pour votre réponse et aide

au niveau de la question 2 PGCD(x,y)=2
on a 2 divise x et 2 divise y  pourquoi ne pas ajouter que (4 ne divise pas x et y ) et (8 pas divise pas x et y ) comment trouver la valeurs commune
et comment le traduire en congruence

pour le cas du PGCD( x,y)=4  on a 4 divise x et 4 divise y  et 8 ne divise pas  et y
et comment le traduire en congruence

est ce qu on doit résoudre un système

si possible de me répondre

merci infiniment