Inscription / Connexion Nouveau Sujet
physique et tableur (excel)
Bonjour à tous,
N'étant pas un pro d'excel j'aurais besoin d'aide sur un exo ou il faut se servir d'excel!
Voilà l'exo:
Vincent a filmé le lancer d'une boule de pétanque de centre G de masse m = 550g. Le film numérisé a été ensuite analysé par un logiciel qui a ermis de pointer l'abscisse x et l'altitude de la boule y toute les t = 40ms. Ces valeurs sont ensuite traitées à l'aide d'un tableur.
Je précise que la trajectoire de la boule est "en cloche"
Après une petite étude de la trajectoire on me demande:
a) Quelles formules Vincent a-t-il écrites dans la ligne du tableur (ou il y a le "E" sur l'image) pour calculer sur la ligne 4:
- la vitesse instantanée v de la boule
- son énergie cinétique Ec
- son énergie potentielle Ep (préciser le niveau de référence choisi)
- l'énergie totale E = Ec + Ep
b)Pourquoi il n'y a pas de valeurs lignes 3 et 17 ?
voilà. En faite, c'est surtout pour les formules Excel que j'ai besoin d'aide particulièrement pour la vitesse instantanée ? Je vois pas comment faire avec l'abscisse x et l'altitude y ?
Si quelqu'un connait un peu Excel utilisé pour la physique si vous pouviez m'aider !
Merci par avance
Merci!
Alors une vitesse intantannée se calcule comme une vitesse moyenne entre deux instants qui encadrent l'instant considéé soit pour un instant P2 par exemple:
Vinst = P1P3/t3-t1)
Mais je vois pas comment appliqué ça dans cet exerice ?!
Merci de m'aider!
Très bien !
C'est ce dont tu as besoin pour la première question.
Je fais le facile... 
le (t3 - t1) de ta formule va devenir sous Excel : A5 - A3
Es-tu d'accord avec cela ?
Maintenant il faut trouver comment écrire sous Excel la distance P1P3
Quelles sont tes idées ? Même si ce n'est pas écrit "sous Excel", si c'est écrit avec les symboles habituels des maths ou de la physique...

Oui, ça je suis d'accord! C'est en effet plutôt la partie P1P3 qui me pose problème.
Pour trouve la distance P1P3, par exemple, je pensais que cela revenait au même de faire P3 - P1 qui j'aurais calculé en faisant:
 [Px(3)²+Py(3)²] -
[Px(3)²+Py(3)²] -  [Px(1)²+Py(1)²]
[Px(1)²+Py(1)²]
Mais je crois que c'est faux parce que j'ai essayé de la faire avec des valeurs du tableur (par exemple ligne 6) et je trouvais pas la même valeur pour la vitesse 
Merci encore !
Cela a un air de ressemblance...
Soit deux points connus par leurs coordonnées
A (x1 ; y1)
B (x3 ; y3)
Quelle formule utilises-tu pour connaître la distance [AB] ?


Voici donc la formule qu'il faut rentrer dans la case D4.
Tu me dis si tu comprends...
=RACINE((B5-B3)*(B5-B3)+(C5-C3)*(C5-C3))/(A5-A3)

Cellule D4
=RACINE(((B5-B3)/(A5-A3))^2 + ((C5-C3)/(A5-A3))^2)
Cellule E4
=1/2*0,55*D4^2
Cellule F4
=0,55*9,81*B4
Cellule G4
=E4+F4

Oui, d'accord ! C'est très clair!
Ca paraît plus facile comme ça! Merci! PAr contre le racine se met comme vous l'avez fait dans la barre ?
Et pourriez-vous vérifiez les formules que j'ai fait pour les autres questions ?
pour son énergie cinétique Ec: 1/2mv² donc 0.275*D4*D4
pour l'énergie totale E = Ec + Ep: E4 + F4
pour son énergie potentielle Ep: m*g*zG je sais que quand on utilise l'énergie potentielle de pesanteur il faut toujours choisir un niveau de référence. Je pense qu'il faut prendre le premier point de la trajectoire quand il lance la boule. Ainsi ça serait: 0.550*9.8*B4
Merci beaucoup pour votre aide!
Bonjour J-P
Ça n'est pas très optimisé...
D'autre part ce contenu de F4 ne permet pas de retrouver exactement l'exemple donné par Arkange.


Tu as parfaitement compris et surtout tu as très bien écrit !
Il ne faut pas écrire les carrés comme D4^2 c'est très long en machine et beaucoup moins précis que D4*D4
Je te félicite !
Pour t'aider si tu n'as pas de tableur chez toi

Pourquoi n'y a-t-il pas de valeurs lignes 3 et 17 ?
Je te confirme que tes valeurs (message de 14 h 13) sont toutes bonnes. En particulier le 9,8 permet de retrouver les valeurs de ton tableau, ce que ne permet pas 9,81

A la ligne 3 je pense que c'est parceque cela doit correspondre au point de lancement de la boule donc sa vitesse est nulle et son énergie cinétique aussi. Mais aussi parce que il manque un point pour calculer la vitesse à lagne 3 et 17 puisqu'il faut deux points qui encadrent l'instant considérés.
Je suis pas sûr de ce que je raconte là ?
Tu as trouvé !
Dans la cellule D4 on écrit une formule qui utilise les valeurs des lignes 3 et 5 (A3, B3, C3, A5, B5 et C5) : donc on ne peut pas mettre la même formule en D3 puisqu'il n'y a pas de valeurs ligne 2 ni en D17 car il n'y a pas de valeurs ligne 18.
Tu as vu que j'ai dû ajouter une valeur (un peu étonnante d'ailleurs) pour la case C17 sinon je n'aurais pas pu trouver une vitesse de 3,06 m/s dans la case D16
D'autre part la ligne 6 est maintenant totalement remplie. Je suppose que ton exercice te le demande.
Je dois quitter l'  dans un quart-d'heure. As-tu des questions ?
dans un quart-d'heure. As-tu des questions ?

Oui l'exercice le demande en effet! Et non je n'ai pas d'autres questions pour le moment! J'ai compris.
Meric beaucoup pour l'aide (très appréciée) 
Avec l'esprit d'escalier... non, la valeur ajoutée à la case C17, (environ 1,6) n'a rien d'étonnant !

Une fois n'est pas coutume, je ne suis pas Cool dans ses remarques.
Je veux bien modifier la Cellule F4
=0,55*9,8*B4
Et alors tout colle avec le tableau de l'énoncé.
Pour le reste, je ne suis pas d'accord.
Optmiser une formule, peut certes faire gagner du temps de calcul à Excel.
C'est important si le temps machine est long devant les manipulations humaines, ce n'est pas le cas ici.
Ici, l'exercice étant didactique, il ne sert à rien d'optimiser l'écriture d'une formule et c'est même néfaste si cette optimisation diminue la compréhension qu'on a de la formule au simple coup d'oeil. (sauf si l'optimisation du temps de calcul est un but de l'exercice, mais cela ne transparait pas dans l'énoncé).
L'avantage d'écrire
=1/2*0,55*D4^2
Plutôt que 0,275 * D2*D2 est que on voit sauter aux yeux la formule = 1/2 m v² et dès lors, cela facilite la correction d'erreurs éventuelles dans le programme. (C'est ici sans grande importance, tant le programme est simple, par contre lorsqu'il s'agit de debugger un programme complexe, cela aide énormément d'avoir des écritures de formules "parlantes".
Le fait d'utiliser D2*D2 au lieu de D2^2 pour une question de précision ne se justifie ici en rien non plus.
Tous les résultats sont limités à 2 décimales (ou 3 chiffres significatifs) et excel calcule avec au moins 13 chiffres significatifs (si mes souvenirs sont bons), que l'algorithme puissance soit moins précis que celui de la multiplication n'a donc ici aucune espèce d'importance.
Même sans cela, la différence entre écrire D2*D2 et D2^2 est illusoire.
exemple:
On entre 17,1548951178145 dans D2
et Excel donne comme résultat:
D2*D2 = 294,2904265032160
et
D2^2 = 294,2904265032160
L'imprécision est la même dans les 2 notations.
Alors que dire si l'affichage est limité à 2 décimales ?
Soit, je ne vois pas les choses comme Coll dans un tel exercice, mais ma divergence de vue avec lui est cependant très marginale.
-----

Juste pour info, voila une copie écran de ce que donne Excel avec les formules que j'ai données (avec g = 9,8 m/s²)
Et bien entendu en choisissant un format de cellule affichant des nombres avec les décimales voulues.
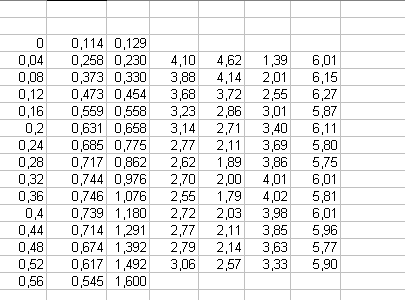

Bonjour J-P
C'est en effet très marginal. Simple habitude de bien écrire. Il n'est pas difficile de prouver les dégâts de l'écriture x^2. Même Microsoft a mis en garde les utilisateurs. Je sais bien qu'avec 32 et 64 bits, avec les vitesses actuelles, cela n'intéresse plus grand monde...
Il reste que j'ai du mal à comprendre l'intérêt d'élever ainsi deux fois au carré (A5 - A3) pour en prendre ensuite la racine carrée. Lisibilité ?

Bonjour à tous,
voila j'ai un exercice de physique et il a deja été traité sur l'ile par des correcteurs et modérateurs...
Voici le lien: ![]() physique et tableur (excel)
physique et tableur (excel)
Seulement j'ai une question supplémentaire à traité:
Quelle conclusion Vincent a t-il pu tirer de ces mesures ??
Merci d'avance, j'ai bien regardé le sujet traité sur l'ile mais je ne vois pas du tout la réponse
*** message déplacé ***
Concernant l'énergie mécanique je ne vois que 2 réponses:
-l'énergie mécanique c'est le résultat de la somme entre l'énergie cinétique et l'énergie potentielle de pesanteur
- l'énergie mécanique de G5 - celle de G4 = 0.14= WAB (theoreme du cours)
Or quand je calcule W: m*g*(Za-Zb)=0.21, donc l'énergie mécanique n'est pas tout à fais égale à W
Tu cherches quelque chose de trop compliqué.
Regarde comment varie l'énergie cinétique (colonne E)
Regarde comment varie l'énergie potentielle (colonne F)
Regarde comment varie l'énergie mécanique (colonne G)
Aux inévitables erreurs de mesure près... que peux-tu conclure pour l'énergie mécanique ?

Alors, je calcule les variations  E pour Ec, Epp et Em en me basant sur les lignes 4 et 5 (donc 5-4, etc)
E pour Ec, Epp et Em en me basant sur les lignes 4 et 5 (donc 5-4, etc)
 Ec 4.14-4.62=-0.48
Ec 4.14-4.62=-0.48
 Epp=2.01-1.39=0.62
Epp=2.01-1.39=0.62
 Em=0,14
Em=0,14
Calculons si  Ec +
Ec +  Epp =
Epp =  Em
Em
-0.48 + 0.62 = 0.14
Ca tombe juste
Donc on peut conclure que la somme de la variation de l'énergie cinétique et de l'énergie de pesenteur est égale à la variation de l'énergie mécanique
Exact.
Encore plus simple, et qui se déduit de ce que tu viens d'écrire correctement :
. les variations de l'énergie potentielle de pesanteur et celles de l'énergie cinétique se font en sens inverse l'une de l'autre de manière telle que l'énergie mécanique reste constante.

D'accord merci beaucoup, j'ai encore un autre exercice de physique à faire, je vais voir si j'arrive à m'en sortir tout seul 
A tout à l'heure peut être...



