Inscription / Connexion Nouveau Sujet
Points alignés (Rotation)
Bonjour, j'ai besoin d'aide.
Merci d'avance.
Sur la figure ci-dessous, ABCD est un carré de sens direct, les triangles DCJ et BCI sont équilatéraux et de sens direct.
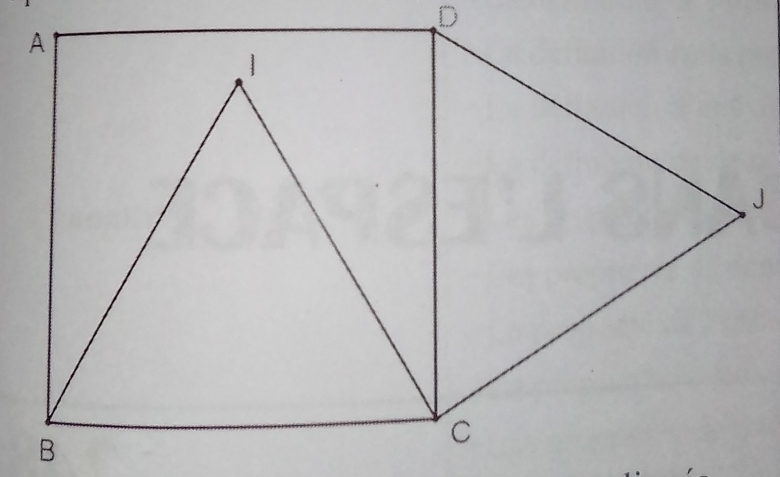
Démontrer que les points A , I et J sont alignés et que IJ=BD.
On pourra construire le point K tel que le triangle AKC sont équilatéral de sens direct puis utiliser la rotation r de centre C et d'angle π/3.
Bonjour,
tu fais plusieurs exos en même temps ?
(le précédent n'est pas terminé correctement)
"On pourra construire le point K tel que.."
bien ... le tracer ce point K 
c'est cela qui permettra de démontrer ce qu'on demande
K n'est pas à mettre une fois l'exo terminé en guise de simple décoration...
*Bonjour,*
Il est possible de tracer un cercle de centre B et de rayon BI ainsi qu'un autre de centre C de même rayon, et ...
Bonjour,
@IRL,
L'énoncé indique une méthode. Autant essayer de l'utiliser.
Par ailleurs, l'usage sur l'île est d'éviter d'intervenir quand un membre a déjà commencé à aider.
Sauf en cas d'absence de réponse de sa part pendant une période conséquente, ou si vraiment il ne va pas dans la bonne direction 
???
on attend ta figure avec le point K explicitement tracé et le raisonnement explicitement rédigé qui à partir de ce point K va permettre de prouver ce qu'on demande.
Bonsoir,
mathafou, dis-moi si je m'incruste.....
othnielzue23, on te suggère la rotation de centre C et d'angle  /3
/3
Par cette rotation, tu as les images de pas mal de points, vu le nombre de triangles équilatéraux de sommet C.
Oui bien sur,
ma remarque initiale était juste pour dire
"c'est toi qui vois si tu es assez solide mentalement pour faire deux choses en même temps sans te mélanger les pinceaux".
moi je suis prêt à attendre, ou tu peux démarrer c'est toi qui vois.
D'accord ,
Alors c'est terminé là bas ...
Je me lance ici .
Voilà la figure (AKC est un triangle équilatéral de sens direct).
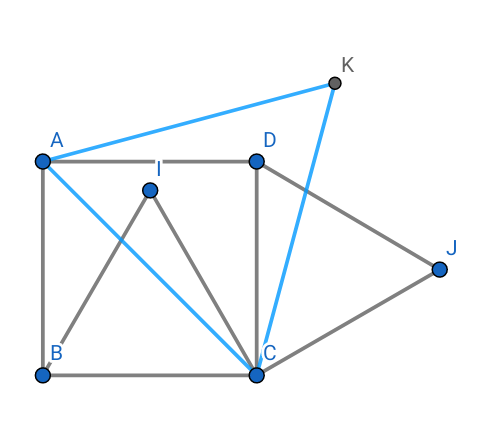
r(C;π/3)(K)=A car Mes(CK;CA)=π/3 , r(C;-π/3)(D)=J car Mes(CD;CJ)=-π/3 et r (C;-π/3)(B)=I car Mes(CB;CI)=-π/3
faux , il est de sens indirect.
et il faut utiliser partout la même et unique rotation (celle indiquée dans l'énoncé)
sinon que pourrait on bien obtenir avec un mélange de rotations dans un sens et dans l'autre ? rien du tout !
Oups désolé ,
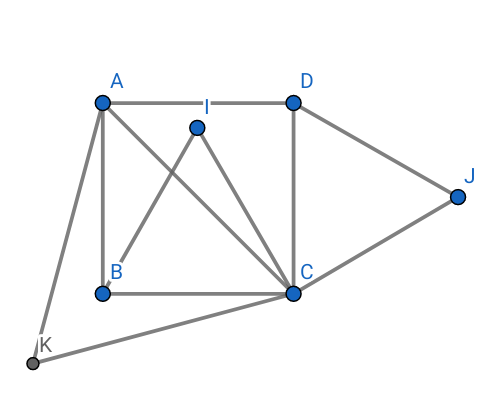
r(K)=A (car mes (CK;CA)=π/3) , r(B)=I (car mes(CB;CI)=π/3) et r(D)=J (car mes(CD;CJ)=π/3)
Oui , plutôt
r(K)=A (car mes (CK;CA)=-π/3) , r(B)=I (car mes(CB;CI)=-π/3) et r(D)=J (car mes(CD;CJ)=-π/3)
Merci
toujours FAUX
tu est trop fatigué pour penser sainement !!!
r(A) = K car mes (CA; CK) = +pi/3
etc
bonne nuit.
Bonjour,
Deux remarques :
Écrire une mesure d'angle pour justifier une égalité du type r(M) = N ne suffit pas.
Il faut aussi une égalité de longueur.
Ici, on peut utiliser cette propriété :
Si MNP est un triangle équilatéral direct alors le point N est l'image du point M par la rotation de centre P et de mesure  /3.
/3.
La rotation conseillée par l'énoncé n'est pas la plus pratique ; mais bon, il faut être docile 
Bonjour Sylvieg,
c'est quasiment la définition de "triangle équilatéral direct"
bref il suffit juste d'être suffisamment (encore ou déja) éveillé pour ne pas se prendre les pieds dans le tapis en mélangeant les noms de points ou le sens de rotation.
quant au choix de la rotation de l'énoncé son seul avantage est justement d'être la simple traduction de "triangle équilatéral direct"
parce que en ce qui concerne la preuve de l'alignement, faire cette preuve dans le sens du raisonnement de l'analyse du problème , ou la faire dans le sens de la synthèse, c'est kif kif :
étant donnée une propriété P conservée par une transformation T
si des points ont la propriété P, alors leurs images ont la propriété P
c'est le sens logique d'un raisonnement rationnel
alors que l'énoncé suggère d'utiliser :
si les images ont la propriété P alors les antécédents ont la propriété P
mais comme je dis, c'est kif kif , vu que en fait :
des points ont la propriété P si et seulement si leurs images ont la propriété P
Bonjour , désolé
Les triangles AKC , BCA et CJD sont des triangles équilatéraux de sens direct.
r(A) = K car mes (CA; CK) = π/3
r(I) = B car mes (CI; CB) = π/3
r(J) = D car mes (CJ; CD) = π/3
Donc les points A, I et J sont alignés (car les points KBD images respectifs des points A , I et J sont aussi alignés)
Merci beaucoup.
r(A) = K
si tu justifies en détail, au lieu de dire simplement que c'est "par définition de triangle équilatéral direct",au moins que ce soit complètement :
car mes (CA; CK) = π/3 et |CA| = |CK|
déja dit ailleurs dans tes exos que la seule valeur de l'angle ne suffit pas à affirmer que c'est une rotation.
oui mais pourquoi, explicitement, les points KBD sont ils alignés ?
si on ne fait que l'affirmer sans preuve, ta démonstration ne tient pas .
Les normes bien sûr ...
Les triangles AKC , BCA et CJD sont des triangles équilatéraux de sens direct.
r(A) = K car mes (CA; CK) = π/3 et |CA|=|CK|
r(I) = B car mes (CI; CB) = π/3 et |CI|=|CB|
r(J) = D car mes (CJ; CD) = π/3 et |CJ|=|CD|
Or r(A)° r(I) °r(J)=r(C;π) car r(A)° r(I) °r(J) est la composée de trois rotations de même centre :C et de même angle π/3.
π/3×3=π donc les points K,B et D forment une droite donc les points K , B et D sont alignés.
Les points K, B et D étant les images des points A , I et J , alors les points A ,I et J sont alignés.
Pour IJ=BD ,
Çà se trouve ici
r(I) = B car mes (CI; CB) = π/3 et |CI|=|CB|
r(J) = D car mes (CJ; CD) = π/3 et |CJ|=|CD|
Donc la rotation de centre C et d'angle π/3 transforme le segment [IJ] en [BD]
==> IJ=BD
r(A)° r(I) °r(J)=r(C;π)
r(A) n'est pas une rotation mais le point K. De même r(I) et r(J) sont des points.
Ton message de 10h51 était plus proche de quelque chose de correct :
r(A) = K
Soit
Les points A, I et J sont les images des points K, B et D par
Il reste à justifier que les points K, B et D sont alignés.
Et inutile de mettre ces | | autour de longueurs.
en passant ..
écrire des |...| ici (sur  ) permet juste d'insister sur la différence entre
) permet juste d'insister sur la différence entre et
si on n'écrit pas en LaTex (sinon comment distinguer IJ de IJ ??)
évidement si on écrit des vrais vecteurs (en LaTeX, ou si on dit "en vecteurs", ou si aucune ambiguïté n'est possible) ces |...| sont totalement inutiles.
D'accord,
Il reste à justifier que les points K, B et D sont alignés.
Mais là ça coince vraiment...
Cherche un peu. C'est de la géométrie de collège.
Si tu ne vois pas, refais une figure moins encombrée, avec le carré ABCD et le triangle ACK, et rien d'autre.
Oups
(BD) est une médiane du triangle AKC car (BD) est une diagonale du carré ABCD donc le milieu de ce carré est le milieu de [AC] et AKC est un triangle équilatéral
C'est trop confus.
Utilise deux phrases séparées pour ne pas mélanger un donc avec un car dans la même phrase.
AKC est un triangle équilatéral,
(BD) est une diagonale du carré ABCD donc le milieu de ce carré est le milieu de [AC].
Donc (BD) est une médiane du triangle AKC.
(BD) est une diagonale du carré ABCD donc le centre de ce carré est le milieu de [AC] et de [BD]
"Donc (BD) est une médiane du triangle AKC" : Non démontré.
Médiane d'un triangle : Droite joignant un des trois sommets du triangle au milieu du côté opposé.
Tu n'as pas démontré que (BD) passe par K.
Tu as parlé de hauteur, de médiane. Quelle est le type de droite remarquable que tu n'as pas invoqué ?
Oui.
Pourquoi la droite (BD) est-elle une médiatrice du triangle AKC ?
Et pourquoi passe-t-elle par K ?
Ne cherche pas midi à quatorze heures. Je répète que c'est niveau collège.
AKC est un triangle équilatéral,
(BD) est une diagonale du carré ABCD donc le milieu de ce carré est le milieu de [AC].
Donc (BD) est en même temps une médiane et une médiatrice du triangle AKC car passe par le point K et par le milieu du côté opposé au point K et est la bissectrice de l'angle
==> Les points K, B et D sont alignés.
(BD) est en même temps une médiane et une médiatrice du triangle AKC car passe par le point K

Ce devrait être la conclusion de ta démonstration.
Et ton histoire de bissectrice, non démontrée, est hors sujet.
Bon :
ABCD est un carré ; donc ses diagonales se coupent en leur milieu et sont perpendiculaires (elles ont aussi la même longueur, mais ça ne sert pas ici).
(BD) est donc la médiatrice de [AC].
Le triangle ACK est équilatéral, donc isocèle en K. Sa médiatrice (BD) passe donc par le sommet K.
Une autre manière sans parler de triangle :
Le point B vérifie BA = BC.
Le point D vérifie DA = DC.
Le point K vérifie KA = KC.
Les trois points B, D et K sont donc tous les trois sur la médiatrice de [AC].
(BD) est en même temps une médiane et une médiatrice du triangle AKC car passe par le point K
Après tout ceci , (BD) une hauteur du triangle AKC , car AKC est un triangle équilatéral.



