Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Autre GéométrieTopics traitant de géométrie [tout]Lister tous les topics de mathématiques
Niveau autre
Partager :

Points intersection sphère et cône en son centre

Posté par
biotah 20-06-14 à 07:49

Bonjour,

je souhaite savoir comment déterminer les coordonnées (Xi;Yi;Zi) de points Pi (ou l'équation correspondante) qui se trouve à la surface d'une unit-sphère de centre O=(0;0;0) et sur la surface d'un cône centré en un point M (Xm,Ym,Zm) dont l'apex est en O, avec un semi-angle théta.

Je ne connais pas tous les termes : centré en un point M = l'axe passant pas l'apex du cone et le centre du "cercle se trouvant à son extrémité" peut être décrit par OM (j'espere que je suis clair).

Le but est de pouvoir représenter graphiquement ce cone sur ma sphère (à partir d'une équation ou de simulations de points rapprochés). J'ai vu pas mal d'équations de cône mais centré sur l'axe des z ce qui ne correspond pas à ma situation (et n'étant pas mathématiciens, j'ai du mal à les adapter).

Merci.

Posté par
idmre : Points intersection sphère et cône en son centre 20-06-14 à 10:27

Salut,

Citation :
je souhaite savoir comment déterminer les coordonnées (Xi;Yi;Zi) de points Pi (ou l'équation correspondante) qui se trouve à la surface d'une unit-sphère de centre O=(0;0;0) et sur la surface d'un cône centré en un point M (Xm,Ym,Zm) dont l'apex est en O, avec un semi-angle théta.


incompréhensible... que veux tu précisément ? déterminer l'ensemble des points qui appartiennent au cône et à la sphère ?

Posté par
biotahre : Points intersection sphère et cône en son centre 20-06-14 à 10:53

oui c'est ça

Posté par
idmre : Points intersection sphère et cône en son centre 20-06-14 à 10:58

Et bien en observant brièvement ce qui se passe et en faisant un dessin ça devrait le faire non ??

Posté par
DOMOREAPoints intersection sphère et cône en son centre 20-06-14 à 11:23

Bonjour,
C'est certain! ... il faut décoder.

Si j'ai bien compris M est un point de l'espace, ton cône est d'axe OM, son sommet est en O , son demi angle est \theta, La sphère est de rayon 1

L'ensemble points cherchés est l'intersection de 2 plans parallèles (P1) et (P2) et de la sphère. c'est donc un ensemble de 2 cercles
Le plan (Pi) pour vecteur orthogonal \vec{OM}

Il passe par le point Hi de (OM) tel que \vec{OH}=(-1)^i\times \frac{\vec{OM}}{||\vec{OM}||} cos(\theta]

Les équations de ces plans sont donc x_M X+y_M Y+z_M Z+D_i=0

En notant m la norme de \vec{OM} c'est à dire m=\sqrt{x_m ^2+y_M ^2 +z_M ^2}

Le point Hi a pour coordonnées (\frac{x_M}{m} cos(\theta);\frac{y_M}{m} cos(\theta),\frac{z_M}{m} cos(\theta))
le point H2 a pour coordonnées ((-1)\frac{x_M}{m} cos(\theta);(-1)\frac{y_M}{m} cos(\theta),(-1)\frac{z_M}{m} cos(\theta))

donc D_i=(-1)^{i+1} mcos(\theta)  tu trouves Di en remplaçant dans l'équation du plan les lettres (X,Y,Z) par les coordonnées de Hi

Le plan (Pi) a donc pour équation x_M X+y_M Y+z_M Z-(-1)^{i+1} mcos(\theta)=0
L'ensemble cherché est ainsi la réunion de deux cercles de l'espace  de centres respectifs Hi de rayon sin(\theta) et situés respectivement dans les plans Pi
  J'espère que ce que je t'ai écris, te parle sinon tu pourras faire une figure en dimension 2 avec un cercle et deux droites sécantes en O formant un angle de mesure 2\theta, pour figurer la sphère et le cône, M est un point quelconque de la bissectrice de l'angle formé par les deux droites,  Les deux droites coupent le cercle en A1,B1 et A2,B2, j'appelle H1 la projection orthogonale de A1 sur OM et P1 le plan de profil figuré par la droite (A1B1)

Posté par
idmre : Points intersection sphère et cône en son centre 20-06-14 à 11:50

Autre méthode:

On considère le cône de semi-angle \theta et d'axe (Oz). L'ensemble des points d'intersection est donné le cercle de rayon \sin\theta centré en (0,0,\cos\theta) dans le plan d'équation z=\cos\theta. Donc il s'agit de \{(\sin\theta\cos\psi,\sin\theta\sin\psi,\cos\theta)\mid \psi\in[0,2\pi[\}.

Considérons maintenant le point M=(\cos\omega\sin\varphi,\sin\omega\sin\varphi,\cos\varphi) qui est sur la sphère avec \omega\in[0,2\pi[ et \varphi\in[0,\pi[. On considère maintenant le cône de semi-angle \theta et d'axe OM. Maintenant les points d'intersection entre le cône et la sphère sont donné par

\left\{\begin{pmatrix}1&0&0\\0&\cos\varphi&-\sin\varphi\\0&\sin\varphi&\cos\varphi\end{pmatrix}\begin{pmatrix}\cos\omega&-\sin\omega&0\\\sin\omega&\cos\omega&0\\0&0&1\end{pmatrix}\begin{pmatrix}\sin\theta\cos\psi\\\sin\theta\sin\psi\\\cos\theta\end{pmatrix}\ \ \Big |\ \theta\in[0,2\pi[\right\}


Pas plus compliqué que ça...

Posté par
idmre : Points intersection sphère et cône en son centre 20-06-14 à 11:51

errata:

\left\{\begin{pmatrix}1&0&0\\0&\cos\varphi&-\sin\varphi\\0&\sin\varphi&\cos\varphi\end{pmatrix}\begin{pmatrix}\cos\omega&-\sin\omega&0\\\sin\omega&\cos\omega&0\\0&0&1\end{pmatrix}\begin{pmatrix}\sin\theta\cos\psi\\\sin\theta\sin\psi\\\cos\theta\end{pmatrix}\ \ \Big |\ {\red \psi}\in[0,2\pi[\right\}

Posté par
DOMOREAPoints intersection sphère et cône en son centre 20-06-14 à 13:13

Bonjour idm,
En effet l'idée de transformer  un cône de position simple par une isométrie est excellente,car elle donner de surcroit  les coordonnées des points alors que je me contentais de définir les ensembles.

Posté par
idmre : Points intersection sphère et cône en son centre 20-06-14 à 13:20

Merci

Posté par
idmre : Points intersection sphère et cône en son centre 20-06-14 à 17:18

Juste une petite rectification de mon post de 11:50, \varphi\in[0,\pi{\red]} (et non pas [0,\pi[)

Posté par
biotahre : Points intersection sphère et cône en son centre 22-06-14 à 22:24

Bonjour,

J'ai testé la méthode avec la matrice. Je part d'un  point M
x[1];y[1];z[1]=(0.6226314;0.006623218;0.7824872)

phi=acos(z[1])
omega=atan2(y[1],x[1])
teta=3*pi/180
psi variant de 0 à 2pi

J'obtiens :
     a           b         c
0.05233300 -0.6213777 0.7817615
0.05232846 -0.6211201 0.7819664
0.05232185 -0.6208626 0.7821714
...
ce qui est pas mal différent de x1...

J'obtiens cette figure avec en rouge le cône pour les résultats brut et en orange si je fais x=-b;y=a et z=c.

Avez vous une explication à cela ? Est ce juste si j'inverse comme ça ?

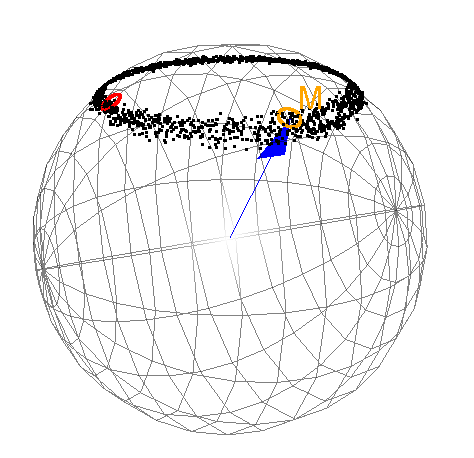
Points intersection sphère et cône en son centre

Posté par
idmre : Points intersection sphère et cône en son centre 22-06-14 à 22:45

ouhla, ça vire chocolat...
je ne comprend déjà pas ton ensemble de point en noir...

ce serait déjà bien que tu nous donne les valeurs exact et non les approximations numérique....

Posté par
biotahre : Points intersection sphère et cône en son centre 22-06-14 à 23:43

Désolé pour les points noirs, ce sont d'autres données que j'ai. Ce sont des valeurs exactes je crois.
Le résultats semblent pas mal (un cercle est formé sur la surface de la sphère) mais ce cercle est centré par rapport à M seulement si je prends les résultats ainsi : x=-b;y=a;z=c => cercle orange (et pas comme le cercle bleu x=a;y=b;z=c)

Image sans les points noirs avec le centre de la sphère O, le points M et la flêche en bleu montrant l'axe du cône. Les cercles bleus et oranges sont les résultats du calcul matriciel "interprêtés" différemment.

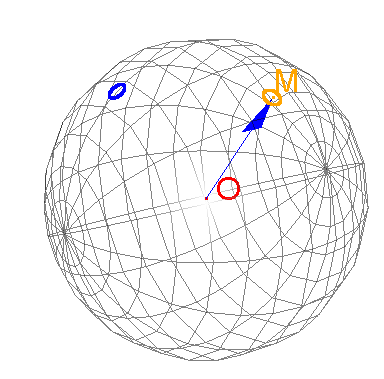
Points intersection sphère et cône en son centre

Posté par
idmre : Points intersection sphère et cône en son centre 23-06-14 à 08:26

Citation :

Les cercles bleus et oranges sont les résultats du calcul matriciel "interprêtés" différemment.

déjà, ça commence mal...

Après, utilises les coordonnés sphérique comme il faut ? Je pense que l'erreur viendrais plus du point M. Peux tu balancer le code que j'y jette un oeil ?

Posté par
idmre : Points intersection sphère et cône en son centre 23-06-14 à 08:55

ouhla ouhla...
c'est normal, j'ai inversé les deux matrices

\left\{\begin{pmatrix}\cos\omega&-\sin\omega&0\\\sin\omega&\cos\omega&0\\0&0&1\end{pmatrix}\begin{pmatrix}1&0&0\\0&\cos\varphi&-\sin\varphi\\0&\sin\varphi&\cos\varphi\end{pmatrix}\begin{pmatrix}\sin\theta\cos\psi\\\sin\theta\sin\psi\\\cos\theta\end{pmatrix}\ \ \Big |\ {\red \psi}\in[0,2\pi[\right\}

devrait mieux marcher

Posté par
biotahre : Points intersection sphère et cône en son centre 23-06-14 à 21:53

Merci pour tes réponses. Je dois surement inverser des choses également ...

M=(xM=0.7773637;yM=0.6235667;zM=0.08288697)
teta=3*pi/180=0.05235988
psi=0
phi=acos(zM)=1.487814
omega=atan2(yM,xM)=0.6760539

cos(omega)=0.7800479
sin(omega)=0.6257198
cos(phi)= 0.08288697
sin(phi)=0.996559

sin(teta)=0.05233596
cos(teta)=0.9986295

cos(psi)=1
sin(psi)=0

\begin{pmatrix} 0.7800479 & -0.6257198 & 0 \\0.6257198 & 0.7800479 & 0 \\0 & 0 & 1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\0 & 0.08288697 & -0.996559 \\0 & 0.996559 & 0.08288697 \end{pmatrix}\begin{pmatrix} 0.05233596\\0 \\0.9986295 \end{pmatrix}=\begin{pmatrix} 0.66353664\\-0.74355074 \\0.08277338\end{pmatrix}=\begin{pmatrix} a\\b\\c\end{pmatrix}

xM; yM et zM sont plus près de -b, a et c que de a, b et c.

Posté par
idmre : Points intersection sphère et cône en son centre 23-06-14 à 22:23

j'ai vérifié, ma formule fonctionne,
tu programmes en quoi ? c'est bizarre cette introduction en introduisant M avec des valeurs approchées... tu ne met pas de valeurs exact ? Met précisément ton code, pas tes valeurs approximative !

Posté par
biotahre : Points intersection sphère et cône en son centre 23-06-14 à 22:32

Je travaille sous R. Les valeurs de M sont celles d'un point sur la sphère que j'ai pris au hasard (ici la premiere de x[1],y[1] et z[1] mais je peux partir de n'importe quelle valeur si tu as un ex). Dans mon code je n'utilise pas les mêmes noms de lettre.
Pour la fonction matrix dans R, on entre les valeurs colonne par colonne.

teta=acos(z[1])#équivalent de phi dans la formule
phi=atan2(y[1],x[1])#équivalent d'oméga

b=c()
for (i in seq(0,2*pi,length.out=1000)){
  angle=3*pi/180#équivalent de teta
  angle2=i#équivalent de psi
  a=matrix(c(cos(phi),sin(phi),0,-sin(phi),cos(phi),0,0,0,1),3,3)%*%
   matrix(c(1,0,0,0,cos(teta),sin(teta),0,-sin(teta),cos(teta)),3,3)%*%
matrix(c(sin(angle)*cos(angle2),sin(angle)*sin(angle2),cos(angle)),3,1)
  b=rbind(b,cbind(a[1],a[2],a[3]))
  
}

Posté par
idmre : Points intersection sphère et cône en son centre 23-06-14 à 22:44

honnêtement, je ne connais pas le langage que tu utilises, je ne peux donc pas t'aider, désolé.
Bonne soirée,

Posté par
biotahre : Points intersection sphère et cône en son centre 23-06-14 à 23:08

Ok, je vais essayer de tout re-coder pour voir.

Est ce que tu pourrais me mettre un exemple avec les valeurs de tes matrices en prenant un point M quelconque que tu choisis ?

ça pourrait peut être m'indiquer ou ça bloque...
En tout cas merci pour ton aide, bonne soirée

Posté par
idmre : Points intersection sphère et cône en son centre 23-06-14 à 23:47

commence par M=(0,0,1)...

Posté par
biotahre : Points intersection sphère et cône en son centre 24-06-14 à 04:50

Avec M=(0;0;1), j'obtiens un résultat qui semble correct. Mais a~b~0 donc même quand x=-b et y=a j'ai pratiquement les mêmes points (pas discernable à l'oeil).Je dois toujours "inverser" pour les autres valeurs.

Posté par
idmre : Points intersection sphère et cône en son centre 24-06-14 à 08:36

Je me demande si tu manipule bien les coordonnées sphérique...
Voici l'ordre conventionnel:
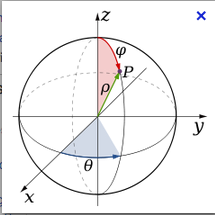
Points intersection sphère et cône en son centre

Par rapport à mes notation, \varphi et \theta correspondent au \varphi de la figure et \omega et \psi au \theta sur la figure.

Posté par
idmre : Points intersection sphère et cône en son centre 24-06-14 à 08:43

en fait, ce qui expliquerais tes résultat ce que tu prend \varphi qui varie de x à z et non pas de z à x (même si ça ne veut pas dire grand, chose, tu comprendra )...

Posté par
lafol Moderateurre : Points intersection sphère et cône en son centre 24-06-14 à 10:31

Bonjour
l'un utiliserait la latitude (normal chez les matheux et les astronomes) et l'autre (idm) la colatitude, ce qui est l'usage chez les physiciens ?

Posté par
idmre : Points intersection sphère et cône en son centre 24-06-14 à 10:37

Lafol: c'est à dire ?

Posté par
lafol Moderateurre : Points intersection sphère et cône en son centre 24-06-14 à 10:44

l'angle phi que tu as représenté est la colatitude
en principe en maths (comme en astronomie et pour repérer des points sur le globe terrestre) on utilise la latitude (de l'extrémité de ta flèche bleue à celle de ta flèche verte)
pour nous qui vivons aux alentours de 45°N, ça ne change pas grand chose, mais en Norvège ou à Gibraltar, un peu quand même ....

Posté par
idmre : Points intersection sphère et cône en son centre 24-06-14 à 10:49

ok, alors je ne suis absolument pas physicien, et moi j'ai toujours utiliser la convention que j'ai mis ici.

Biotah : Pour utiliser la convention de Lafol, il y a pas mal de chose à changer... que je te laisse le soin de le faire

Posté par
idmre : Points intersection sphère et cône en son centre 24-06-14 à 10:50

et c'est d'ailleurs probablement ce qui doit expliquer que l'ensemble ne concorde pas...

Posté par
biotahre : Points intersection sphère et cône en son centre 24-06-14 à 23:40

Pour ma part je suis biologiste, j'ai donc aucune à priori concernant les notations des angles, j'essaye juste de suivre la notation dont on me parle.

Ici idm dit $M=(\cos(\omega)*\sin(\phi),\sin(\phi)*\sin(\omega),\cos(\phi))$ donc on parle de colatitude pour phi et de longitude pour oméga.

ce qui correspond je crois à : $ \phi=\arccos(z)$ et $\omega=\arctan{2}(y,x)$

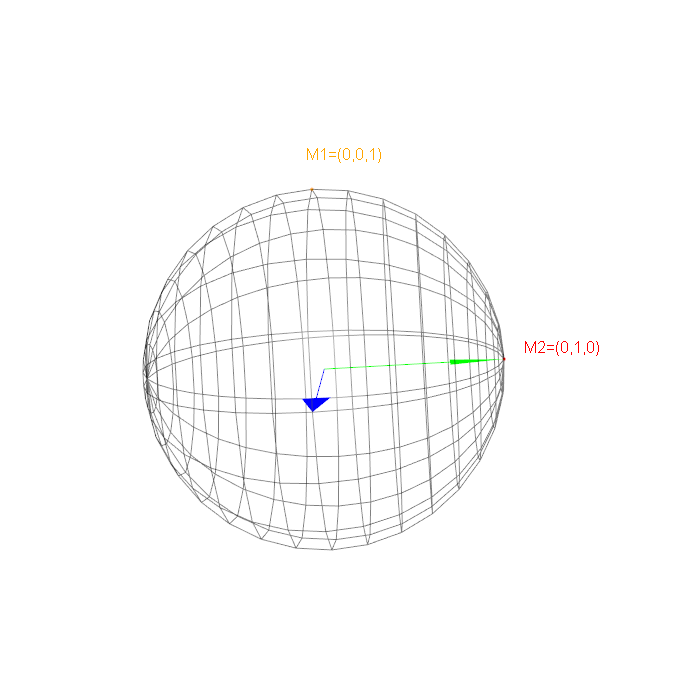
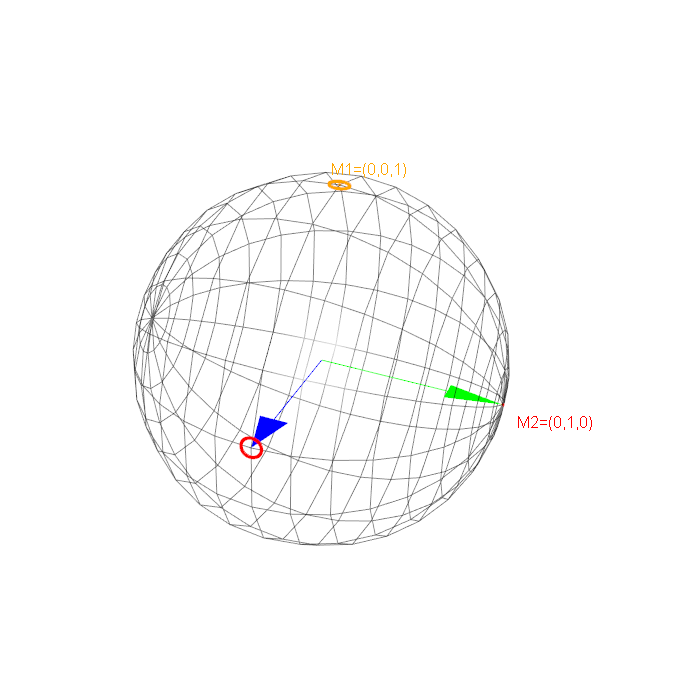
D'après la sphère (image1) ou l'axe des x est en bleu et l'axe des y est en vert :

M1 (0,0,1): omega=0 et phi=0
M2 (0,1,0): omega=90 et phi=90

Calculs :
M1 : omega=atan2(y,x)=0 et phi=acos(z)=acos(1)=0
M2 : omega=atan2(1,0)=pi/2 et phi=acos(0)=pi/2 (soit 90deg)

donc je suis bien en colatitude car les 2 phi (M1-M2) seraient inversés sinon ?!

Maintenant si je rajoute mes calculs à la sphère (image2), le cone rouge de M2 est aligné sur x et non pas y ?

Points intersection sphère et cône en son centre

Points intersection sphère et cône en son centre

Posté par
idmre : Points intersection sphère et cône en son centre 25-06-14 à 06:16

Malheureusement ça ne marche pas comme ça (car ton ordinateur utilise les angles donné par Lafol)... du coup, il faut changer quelques trucs à savoir partir non du cône d'axe (Oz), mais du cône d'axe (Ox), et donc là on a l'ensemble d'intersection n'est plus \{(\sin\theta\cos\psi,\sin\theta\sin\psi,\cos\theta)\mid \psi\in[0,2\pi[\} mais \{(\cos\theta,\sin\theta\cos\psi,\sin\theta\sin\psi)\mid \psi\in[0,2\pi[\} et ensuite appliquer les différentes matrices de rotations (d'abord selon (Ox) et ensuite selon (Oz) ) ce qui donne

\left\{\begin{pmatrix}\cos\omega&-\sin\omega&0\\\sin\omega&\cos\omega&0\\0&0&1\end{pmatrix}\begin{pmatrix}\cos\varphi&0&\sin\varphi\\0&1&0\\-\sin\varphi&0&\cos\varphi\end{pmatrix}\begin{pmatrix}\cos\theta\\\sin\theta\cos\psi\\\sin\theta\sin\psi\end{pmatrix}\ \ \Big |\ { \psi}\in[0,2\pi[\right\}

J'espère que cette fois ci, ce sera bon

Posté par
biotahre : Points intersection sphère et cône en son centre 26-06-14 à 01:03

Merci IDM, malheureusement ça ne marche pas que je sois en colatitude ou en latitude (à l'opposé du points d'intérêt en général). Par contre, en utilisant les anciennes matrices de rotation, ça marche tout le temps si je rajoute pi/2 à la longitude avant les calculs !?

Posté par
fluorhydriquere : Points intersection sphère et cône en son centre 26-06-14 à 06:10

bonjour Biotah
mon post juste pour un truc en rapport avec ce fil

en rapport mais sans interferer dans la discution

en apparté donc là je generalise à \mathbb {R}^n tu prend R3 pour ton fil et applique ça pour ton fil en conséquence

avant il faut juste se mettre en memoire que en fait tout le raisonnement des outils qui suivent et qui te serviront viens des proprietes du produit scalaire euclidien

pour deux vecteurs V et W non nuls mais colineaires ou pas on peut definir un angle \theta dans l'intervalle [0°,180°] qui represente l'angle formé entre ces deux vecteurs non nuls

un peu de temps en trigo en essayant de retrouver le moyen pas tres compliqué pour demontrer que en fait là toutes les infos sur cet angle est donnés par le produit scalaire euclidien on va le noter conventionnellement V.W pour se simplifier la vie et noter V^2=V.V mais ces notations sont trompeuses comme tu le verifiera mais pour ici on fera avec ça on fait toujours selon ce qu'on recherche et toujours en se simplifiant ce qui compte est de savoir que pour ici ça reste correct et qq chose de plus delicat on verra pourquoi une autre fois

bon bref on en arrive avec un peu de demo  à retrouver que (attention ici les vecteurs son non nuls)
la norme d'un vecteur ||V||=\sqrt {V^2} la notation est suspecte mais pour ici ça ira tu doit bien comprendre que VW est un réel tout comme V^2
V.W=0 signifie que l'angle est 90°
V.W>0 signifie que \theta \in [0°;90°[
V.W<0 signifie que \theta \in ]90°;180]
\theta =arccos \frac {VW}{\sqrt {V^2W^2}}
voir comment est arccos son domaine de definition et d'application
cos \theta = \frac {VW}{\sqrt {V^2W^2}}
\displaystyle sin \theta = \sqrt {\displaystyle \frac {V^2W^2-(VW)^2}{V^2W^2}}

tu peut aussi profiter de cette équation facile à demontrer
pour V et W non nuls et non colineaires (attention exclusivement non nuls et non colineaires) alors si
Z=V^2W-(VW)V là encore la notation est suspecte et que là en fait c'est une difference de deux vecteurs construits chacun d'eux par le produit d'un réel par un vecteur

apres tu adoptera une autre notation mais bon pour là ça peut passer
bref donc si Z est ainsi construit alors Z est orthogonal à V et donc VZ=0  

avec tout ça tu as de bon outils quand aux demos elles sont pas mechantes

bon dans R3 une demo pas mechante non plus assez rapide te fera dire que si V est un vecteur non nul et sous certaine conditions (que je te donne en dessous mais qu'une petite demo suffit à voir )alors

V=(v_1,v_2,v_3)=(||V||cos \theta _1cos \theta _2,||V||sin \theta _1cos \theta _2,||V||sin \theta _2)

et en fait les deux angles  
\theta _1 l'angle forme par (1,0,0) et (v_1,v_2,0)
\theta _2 l'angle forme par (v_1,v_2,0) et (v_1,v_2,v_3)

tu peut generaliser dans R^n

mais là bon pour une autre fois c'est pas compliqué une petite demo suffit

bon les cas particuliers tienne tout simplement que definir ces angle oblige que les vecteurs soient non nuls or ces cas arrivent pour (v_1,v_2,0)
même si V n'est pas nul donc bon là rien ne t'empêche de poser telle convention qui fait que:
lorsque v_1=0 et  v_2=0 alors on pose telle valeur pour l'angle et verifie que la formule reste valable en posant ainsi te angles

pour le reste et l'application à ce fil tu as des petits outils là qui te rende le problème plus facile

salut et excusez l'apparté


Rechercher
Menu
Espace membre
33 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1725 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !