Bonjour,

Comme ce que tu décris c'est un triangle fixe, la notion de "maximum" n'existe pas...

il ne peut y avoir maximum que si quelque chose varie.
donc déja pas "un coté de longueur 5" mais un côté défini par un curseur ou un "point sur segment"
Puis à partir de ce segment de longueur essentiellement variable calculer/construire les deux autres de sorte que le périmètre soit imposé = 15. Et le triangle isocèle, et non pas comme le seul que tu as construit équilatéral.

Tu peux alors demander à Geogebra de mesurer l'aire de ce triangle et d'en afficher la valeur en fonction du côté variable ...

mais de là à lui demander de "prouver" quelque chose !
Tu pourras observer et émettre la conjecture que ...
ensuite ce sera à toi de le démontrer.

Merci pour ta réposne si rapide. Ma question suivante est: comment puis-je créer des objets dynamiques comme tu les décris? Il faut apprendre le langage de script de géogebra?

Johnny

non, pas besoin.

tu peux tout faire "en construction géométrique"

par contre savoir utiliser directement les commandes directes de Geogebra (je ne parle pas des scripts) permet un gain de temps et d'efficacité considérable.
Ici tu peux créer les objets suivants (avec les outils, ou les commandes directes) :
Nom Définition

Point A Point en O(0,0)
Point P Point sur axeX définit le périmètre = AP
Segment e Segment [AP]
Point M Milieu de [AP] limite de B
Segment a Segment [AM]
Point B Point sur a point variable astreint à [0, p/2]
Point N Milieu de [BP] la moitié de ce qu'il reste
Cercle c Cercle de centre B et de rayon Segment[N, P]
Cercle d Cercle de centre A et de rayon Segment[N, P]
Point C Point d'intersection de c et d
Triangle poly1 Polygone A, B, C
Nombre s poly1 "cast" du polygone (objet) en valeur de son aire
Point T Point[{x(B), s}] point courant de la courbe
Lieu lieu1 Lieu[T, B] trace la courbe aire en fonction de la position de B

+ quelques gadgets sans importance (comme le segment BT et les côtés même du triangle)



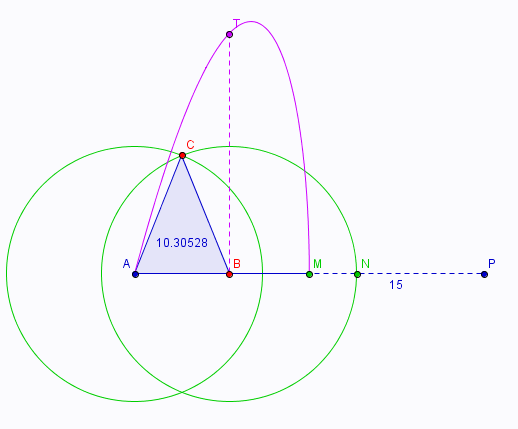
en cliquant droit sur B tu peux demander de l'animer, tout bouge tout seul.
sinon on peut déplacer B à la main sur son domaine de définition [0, p/2] (sur le segment AM)

la clé ici pour faire tracer la courbe est de taper la commande directe de construction du point T :
T = Point[{x(B), s}]
dans la zone de saisie
x(B) est l'abscisse de B, (B est sur l'axe car tout le segment AP y est)
s est la valeur numérique de l'aire à tout instant du polygone "triangle ABC"
On ne peut pas mettre directement
T = Point[{x(B), poly1}] car il comprendrait de mettre T comme point du polygone lui même. On est obligé de "caster" poly1 en un nombre

Merci infinimmet! Avec ton explication, j'ai fini mon exercice, et en plus, j'ai appris {enormement de choses sur Geogebra!

La seule chose que je n'ai pas reussi c'est la tracage du point T (celui que decrit la parabole).

Mais le reste est tout simplement sublime grace á toi!!

Johnny

Pour faire tracer le lieu du point T c'est l'outil "lieu géométrique"

puis cliquer sur T et puis sur B

(incidemment ce n'est pas une parabole)

Parfait, simplement parfait. J'avais installé la version en anglais et je ne pouvais trouver "lieux" (locus, dans la version anglaise).

Une dernière question: as-tu déjà fait des transformations dans le plan complexe C en utilisant Géogébra?

Merci infinimment, encore une fois.


Johnny

Non, je n'ai pas trop utilisé la partie "calculs" de Geogebra.