Inscription / Connexion Nouveau Sujet
Présentation d'une pyramide
Bonjour tout le monde ,
J'aurais besoin d'aide s'il vous plaît pour vérifier ma réponse de ce petit exercice,
je vous remercie par avance.
Une pyramide a pour base un hexagone régulier dans le plan horizontal de projection le coté de cet hexagone est de 3,5cm, le sommet de la pyramide est à la verticale d'un des sommets de la pyramide est à la verticale d'un des sommets de l'hexagone et à 5 cm au-dessus. Représenter cette pyramide.
-calculer le volume de la pyramide précédente
le volume d' une pyramide: V= 1/3hauteur * aire de base
Ici la hauteur est 5 cm.
Il reste à calculer l' aire de la base, autrement dit de l' hexagone.
Nous avons un hexagone régulier dont les six côtés ont tous la même longueur a = 3.5cm.
Soit a : la longueur d'un côté, l'aire A d'un hexagone régulier est égale à :
A=(3√3)/2a²
Aire base hexagonale = 31.82 cm²
Le volume donc sera :
V = (aire base x h)/3
= (31.82 x 5) / 3
= 53.03 cm3
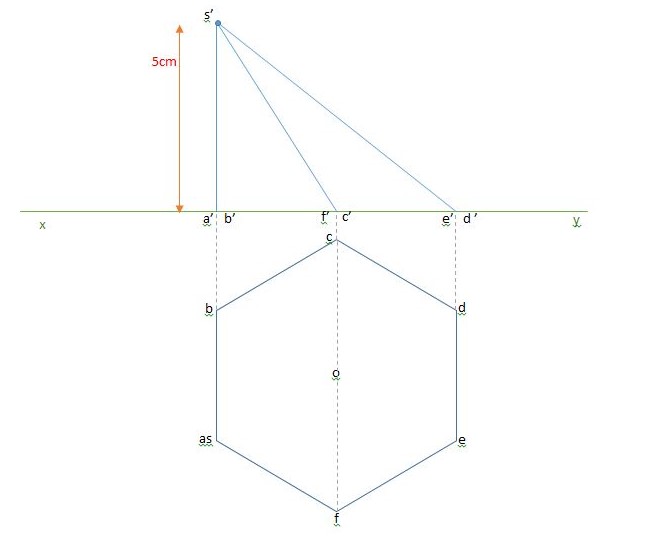
merci mathfou pour la remarque....pour que toutes les arêtes de la pyramide soient distinctement visibles sur l'épure, il faut qu'on tourne l'hexagone d'un petit angle autour de son centre
Non.
pour les arêtes dans un plan de bout (SA et SB) OK (épures confondues avec d'autres)
de même SF aussi est OK (sf = af sur l'épure)
mais les arêtes SC, SD et SE ne sont pas représentées complètement sur ton épure alors qu'elles doivent y figurer
(segments sc, sd et se absents alors qu'ils sont obligatoires, à croire que tu n'as jamais vu une pyramide vu de dessus !)
Merci mathafou.....j'ai compris le principe . .sauf que je n'ai l ordinateur pour l instant. ..si tu peux me faire un tracé stp



 géométrie en post-bac
géométrie en post-bac