Bonjour
Alors voilà un exercice de probabilité récent m'a rappelé un contrôle que j'avais fait l'année dernière et dont je n'ai toujours pas compris ma faute, bien que le prof ait tenté de m'expliquer.

Je n'ai pas d'exercice à faire, de DM à rendre ou de contrôle dans les prochains jours. La seule et unique raison qui me pousse à demander de l'aide et des explications ici est l'envie de comprendre.

Les diagrammes de Viennes réalisés sont les miens.
Le diagramme relatif à l'exerce du contrôle de l'année dernière a été validé par le prof.
Les consignes et les question ont été recopiées au mot prés.


Voici l'exercice fait récemment :

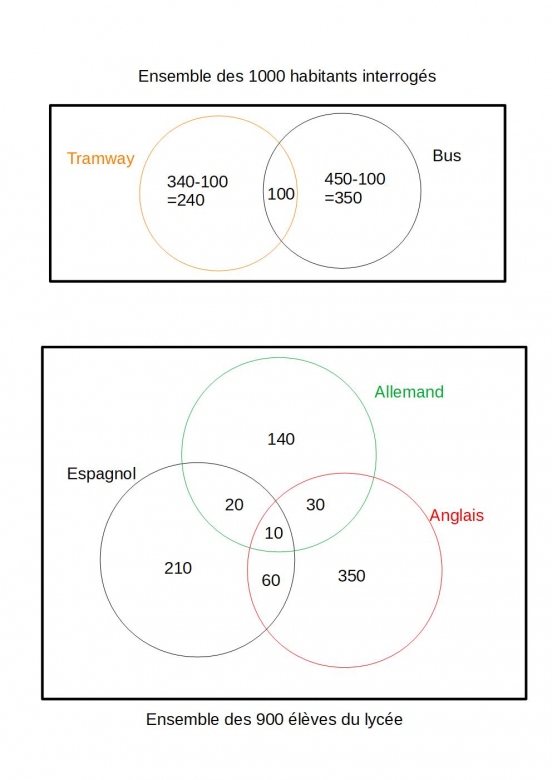
« Une ville ne compte que deux types de transports en commun : le tramway et le bus.
On a interrogé 1000 habitants : 340 déclarent utiliser le tramway, 450 prennent le bus et 100 utilisent les deux moyens de transport.

Calculer la proportion des habitants qui utilisent au moins un des deux moyens de transport. »


Ma réponse :

Soit T l'évènement « l'habitant utilise le tramway »
Soit B l'évènement « l'habitant utilise le bus »

Selon moi l'ensemble recherché est constitué :
des habitants utilisant uniquement le bus + des habitants utilisant uniquement le tramway + les habitants utilisant uniquement le bus et le tramway

Donc cela revient à rechercher P(T U B) = P(T) + P(B) - P(A∩B)
                                                 = 340/1000 +450/1000 - 100/1000
                                                                                          = 690/1000 = 69 %

Mais le prof a dit que la probabilité recherchée était P= (340 + 450)/1000)
                                                                                                                        =790/100 = 79 %

Je ne comprends pas pourquoi il ne faudrait pas enlever 100 habitants car selon moi
340 + 450 = (Nombre d'habitants utilisant le bus + Nombre d'habitants utilisant le bus et le tramway) + (Nombre d'habitants utilisant le tramway + Nombre d'habitants utlisabt le bus et le tramay)
                = Nombre d'habitants utilisant le bus + Nombre d'habitants utilisant le tramway + 2 * Nombre d'habitants utilisant le bus et le tramway

Selon moi on compte deux fois les habitants utilisant les 2 transports donc il serait logique d'enlever 100 pour ne les compter qu'une seule fois




Voici la question du contrôle de l'année dernière avec une question très similaire :

L'exercice avait  déjà était donné en classe (exactement le même avec les mêmes valeurs), seulement une ou 2 nouvelles questions nous attendait au contrôle. J'ai donc réalisé le diagramme (qui a été noté juste)  d'après la correction faite en classe, bien que je le pensais ambigu à cause de la consigne.
(Oui je pense que de mettre au contrôle un exercice fait en classe n'est pas d'une grande utilité...)

« Un lycée compte 900 élèves. Parmi eux, 450 étudient l'anglais, 200 l'allemand, 300 l'espagnol, 60 l'anglais et l'espagnol, 30 l'anglais et l'allemand, 20 l'allemand et l'espagnol et enfin 10 élèves étudient les 3 langues.

En choisissant un élève au hasard, quelle est la probabilité qu'il étudie l'anglais ou l'espagnol ? »

Déjà des remarques sur la consigne (l'exo est foutu comme ça) :

- dans les 450 élèves d'anglais, il y a :
ceux étudiant uniquement l'anglais + ceux étudiant uniquement l'anglais et l'allemand + ceux étudiant uniquement l'anglais et l'espagnol + ceux étudiant les trois langues.

- dans les 200 élèves d'allemand, il y a :
ceux étudiant uniquement l'allemand + ceux étudiant uniquement l'allemand et l'anglais + ceux étudiant uniquement l'allemand et l'espagnol + ceux étudiant les trois langues.

- dans les 300 élèves d'espagnol, il y a :
ceux étudiant uniquement l'espagnol + ceux étudiant uniquement l'espagnol et l'allemand + ceux étudiant uniquement l'espagnol et l'anglais + ceux étudiant les trois langues.

Mais par contre (ce que je trouve ambigu et source d'erreur) :

- dans les 30 élèves d'anglais et d'allemand, il faut comprendre « 30 élèves étudiant uniquement ces deux langues. »
- dans les 60 élèves d'anglais et d'espagnol, il faut comprendre «60 élèves étudiant uniquement ces deux langues. »
- dans les 20 élèves d'anglais et d'allemand, il faut comprendre « 20 élèves étudiant uniquement ces deux langues. »

Formulé comme ça dans la consigne, c'est pas évident de savoir que les élèves étudiant les 3 langues ne sont pas inclus… Perso c'est du français, j'y aurais inclus les élèves de 3 langues à chaque mais bon l'exo était foutu comme ça.


Voilà ma réponse à la question :

P(Anglais  U EspAgnol)= P(Anglais) + P(Espagnol)- P(Anglais ∩ Espagnol)
                                                   = 450/900 + 300/900 -70/900
                                                  = 680/900

Cependant le prof a mis dans la correction :
P= 450/900 + 300/900 -60/900
  =690/900

Ce que je trouve bizarre ici est que pour moi il compte 2 fois les élèves étudiant les 3 langues car il enlève 60 au lieu de 70…

J'avais demandé au prof qui m'a dit qu'il n'y avait pas de problèmes.
J'avais aussi demandé à d'autre élèves leur avis mais ils m'ont particulièrement agacé :

-ceux ayant répondu comme moi qui ne cherchent pas à comprendre leurs erreurs
-ceux ayant mis comme le prof et se moquant royalement de mes doutes car « j'ai eu bon et pas toi, c'est le prof qui le dit ».


Je vous remercie d'avoir pris le temps de lire et vous remercie d'avance pour votre aide.