Inscription / Connexion Nouveau Sujet
Probabilité urnes et boules
Une première urne, appelée Ua, contient quatre boules rouges et six boules noires. Une seconde urne,
appelée Ub contient une boule rouge et neuf boules noires. Les boules sont indiscernables au toucher.
Un joueur dispose d'un dé à six faces, parfaitement équilibré, numérotées de 1 à 6. Il le lance une fois :
s'il obtient 1, il tire au hasard une boule de l'urne Ua, sinon il tire au hasard une boule de l'urne Ub.
On note A l'événement le joueur tire une boule de l'urne Ua.
On note B l'événement le joueur tire une boule de l'urne Ub.
On note R l'événement le joueur tire une boule rouge.
Le « n » représente l'union parce que je n'arrive pas à le faire.
1) Construire un arbre pondéré traduisant la situation.
2) a) Calculer p(A n R) et p(B n R).
b) Montrer que p(R) = 0,15.
3) a) Calculer pR(A).
b) Si le joueur tire une boule rouge, la probabilité qu'elle provienne de l'urne a est-elle supérieure à la
probabilité qu'elle provienne de l'urne Ub?
4) Le joueur répète 4 fois l'épreuve aléatoire précédente, dans des conditions identiques et
indépendantes (c'est-à-dire qu'à l'issue de chaque épreuve, les urnes retrouvent leur composition
initiale). Calculer la probabilité d'obtenir au moins une boule rouge sur les quatre boules tirées.
1) j'ai fait l'arbre
p(A)=
Donc plus de chance que la boule rouge vienne de l'urne A sauf que je ne suis pas convaincue par ces deux derniers calculs. Est-il normal que je trouve un résultat supérieur à 1 pour pR(A) ?
Merci
Bonjour,
tu peux poster ton arbre ?
non, il n'est pas normal de trouver une proba > 1,
une proba estt toujours comprise entre 0 et 1.
tu dis que tu as écrit n pour union , ce serait pas plutot n pour inter ?
je regarde ton sujet, et je reviens.
Leile
Oui je veux bien le poster mais est-ce que j'ai le droit d'en envoyer une photo ? Comme les règles sont assez strictes je ne voudrais pas faire une bêtise...
Et oui je me suis trompée c'est bien inter
Leile
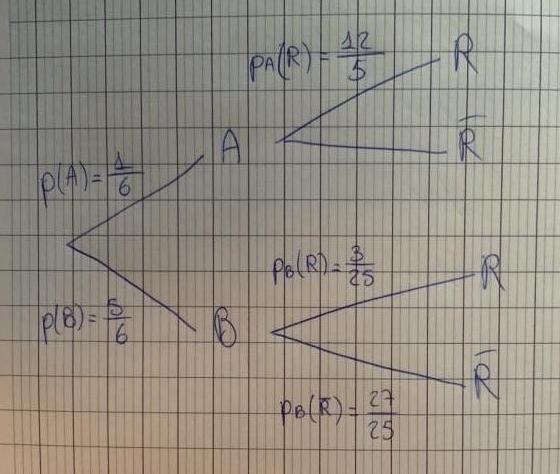
Je viens de me rendre compte que mes données sur mon arbre sont fausses car la somme n'est pas égale à 1
Je suis perdue
c'est bien ce qui me semblait, c'est pour ça que je te demandais ton arbre.
poste le quand même, je te dirai où tu t'es trompée.
tu lances ton dé, tes probas sont OK au début.
je vois que tu as "recalculé" pA(R), alors que c'est donné dans l'énoncé. C'est là que tu te trompes.
tu te places en A, là, l'énoncé te dit : dans l'urne A, il y a 4 rouges sur 10
(c'est donc bien " p(Rouge) sachant qu'on est dans l'urne A")
donc la proba que tu dois écrire de A vers R est 4/10
tu vois ?
sais tu rectifier ton arbre à présent ?
Leile
Merci beaucoup ! J?ai du mal avec cette notion?
Je vous envoie mon nouvel arbre mais elle se met automatiquement à l?envers, désolée?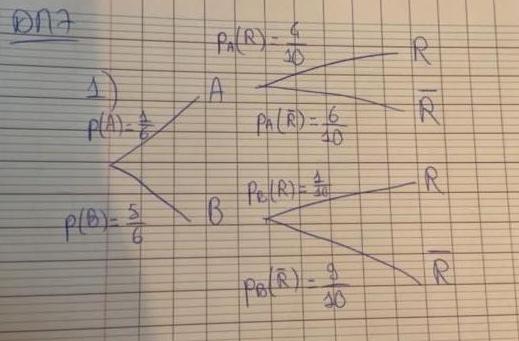
* Modération > Image tournée. Bizarre cette histoire d'à l'envers  *
*
Leile
La probabilité que la boule rouge vienne de l'urne UA est inférieur à la probabilité qu'elle vienne de l'urne UB
OK, alors on ne va pas en parler.
p(R) = 0,15 à chaque jeu et tu refais le même jeu 4 fois de suite.
p(N) = ?
pour avoir moins de calcul à faire, on va trouver la proba de l'évenement contraire à celui qu'on examine.
Quel est l'évenement contraire à "obtenir au moins une boule rouge sur les quatre boules tirées." ??
Je crois que l'évènement contraire est « ne pas obtenir de boule rouge sur les 4 tirées » ?
Que représente p(N) ?
j'ai écrit p(N) pour p(Noire) pour p(Rbarre).
oui, ne pas obtenir de boule rouge, c'est finalement tirer NNNN.
que vaut p(N) ?
et donc que vaut p(N n N n N n N) ?
Si je comprends bien, ça signifie que la probabilité de tomber sur au moins une boule rouge sur 4 tours est de ?
Si je comprends bien, ça signifie que la probabilité de tomber sur au moins une boule rouge sur 4 tours est de
non, ça n'est pas ça.
p(N) = 1 - p(R) = 17/20 d'accord.
N est l'événement contraire de R, donc p(N) = 1 - p(R)
p(aucune boule rouge) = p( N n N n N n N ) = ?
"aucune boule rouge" est l'évenement contraire de "au moins une rouge"
donc p(au moins une rouge) = 1 - p(aucune rouge).
à ce soir.
Leile
J'essaye de comprendre mais je n'y arrive pas car je voulais faire p(N)*4 mais le résultat est plus grand que un
quand tu calcules p(A n R)
tu écris p(A n R) = 1/6 * 2/5 = 2/30 = 1/15
tu as multiplié les probas.
(sur l'arbre, pour calculer la proba d'une issue, tu multiplies toutes les probas que tu trouves sur le chemin qui mène à cette issue.)
ainsi p(N) = 17/20
p( N n N) = 17 / 20 * 17/20 = (17/20)2 ( et non 17/20 * 2)
OK ?
alors à ton avis
p( N n N n N n N) = ?
oui,
p(aucune boule rouge) environ égale à 0,522
il te reste à répondre à la question :
p(au moins une boule rouge) = ?
Et la je peux dire que la probabilité de tomber sur au moins une boule rouge sur 4 tours est de 76 479/160 000 ?
oui,
tu aurais pu écrire aussi
p(au moins une R) ≈ 1 - 0,522
tu vois qu'en passant par l'événement contraire, on a fait peu de calculs.
D'autres questions ?
Merci beaucoup d'avoir pris du temps pour m'aider, tout est clair je n'ai pas d'autres questions. Bonne soirée